պարապմունք 57

Թեմա՝ y=√x ֆունկցիայի գրաֆիկը և հատկությունները։

y=√x ֆունկցիայի գրաֆիկը կառուցելու համար, սովորականի պես, x անկախ փոփոխականին տանք մի քանի դրական արժեքներ (x<0 դեպքում √x իմաստ չունի) և հաշվենք y կախյալ փոփոխականի համապատասխան արժեքները:Հարմարության համար կընտրենք x-ի այնպիսի արժեքներ, որոնց դեպքում ճշգրիտ որոշվում է քառակուսի արմատի արժեքը:Այսպիսով՝ եթե x=0, y=√0=0, x=1, y=√1=1, x=4, y=√4=2, x=6.25, y=√6.25=2.5, x=9, y=√9=3

Արդյունքում, լրացրինք հետևյալ աղյուսակը:

x	0	1	4	6.25	9
y	0	1	2	2.5	3

Կոորդինատական հարթության վրա կառուցենք գտնված (0;0),(1;1),(4;2),(6.25;2.5),(9;3) կետերը: Դրանք գտնվում են որոշ կորի վրա: Գծենք այն: 

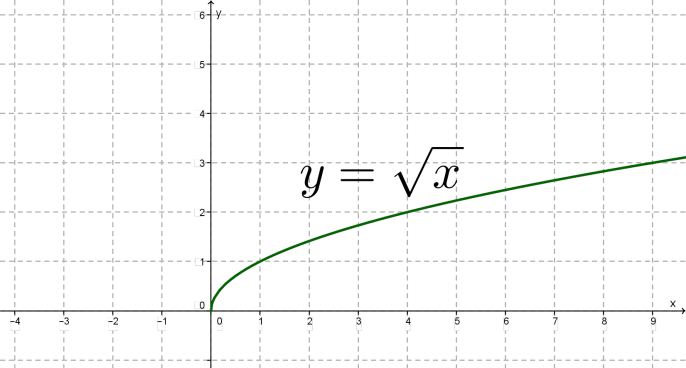
Ստացանք y=√x ֆունկցիայի գրաֆիկը:

Գրաֆիկը շոշափում է oy առանցքը (0;0) կետում:

y=√x ֆունկցիայի հատկությունները թվարկելիս կհիմնվենք կառուցված գրաֆիկի վրա:

1. Ֆունկցիայի որոշման տիրույթը [0;+∞) ճառագայթն է
2. y=0 եթե x=0 և y>0 եթե x>0
3. Ֆունկցիան աճում է [0;+∞) ճառագայթի վրա
4. Ֆունկցիան սահմանափակ է ներքևից, բայց սահմանափակ չէ վերևից
5. Ֆունկցիան ունի փոքրագույն արժեք և չունի մեծագույն արժեք y_min=0, եթե x=0  և y_max գոյություն չունի
6. Ֆունկցիան անընդհատ է [0;+∞) ճառագայթի վրա
7. Ֆունկցիայի արժեքների բազմությունը օրդինատների առանցքի դրական ճառագայթն է՝ [0;+∞)   

Հարցեր և առաջադրանքներ։

1․Ո՞րն է y=√x ֆունկցիայի որոշման տիրույթը։ [0;∞)

2․Արդյոք ֆունկցիան ունի՞ մեծագույն և փոքրագույն արժեքներ։ Ֆունկցիան ունի փոքրագույն արժեք և չունի մեծագույն արժեք։

3․ Որոշել y=√x ֆունկցիայի արժեքը, երբ x=1, x=4, x=9, x=16, x=25:

x=1 y=1

x=4 y=2

x=9 y=3

x=16 y=4

x=25 y=5

4․ Գտնել y=√x ֆունկցիայի արգումենտի այն արժեքը, որի դեպքում y=1, y=3, y=6, y=7, y=10։

y=1 x=1²

y=3 x=9

y=6 x=36

y=7 x=49

y=10 x=100

5․ Պատկանում են արդյո՞ք y=√x ֆունկցիայի գրաֆիկին հետևյալ կետերը՝ A(1;1), B(-2;4), C(4;2), D(36;-6), E(81;9):

A(1;1) այո

B(-2;4) ոչ

C(4;2) այո

D(36;-6) ոչ

E(81;9) այո

6․ Կառուցել ֆունկցիայի գրաֆիկը։ ա)y=√x , բ)y=√-x , գ)y=-√x։

6․ Կառուցել ֆունկցիայի գրաֆիկը։
ա)y=√x 

բ)y=√-x 
x<0 դեպքում √x իմաստ չունի

գ)y=-√x