Պարապմունք 56

Թեմա՝ y=k/x ֆունկցիան և նրա գրաֆիկը։

Դիտարկենք y=2x ֆունկցիան և լրացնենք նրա արժեքների աղյուսակը: 

x	1	2	−1	−2	4	12	−4	−12
y	2	1	−2	−1	12	4	−12	−4

Կառուցենք այս կետերը կոորդինատական հարթության վրա: Ուրվագծվում է երկու ճյուղերից բաղկացած կոր: Տանենք այն:

y=1/x ֆունկցիայի գրաֆիկի պես  այս կորը ևս կոչվում է հիպերբոլ:

Հիմա դիտարկենք k<0 դեպքերից որևէ մեկը, օրինակ՝ k=−1 -ը:

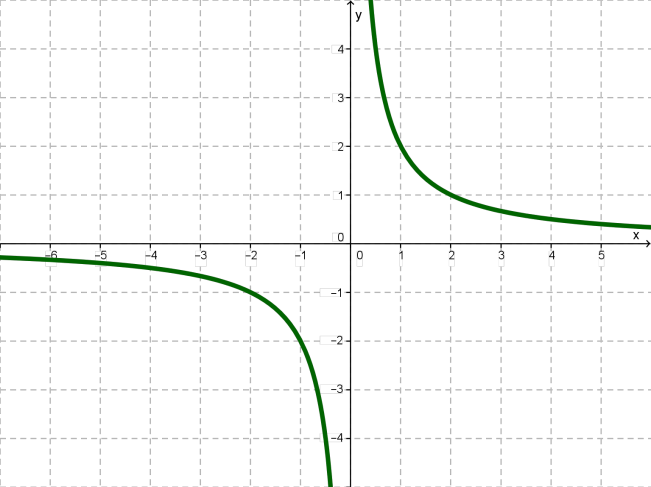
Կառուցենք y=−1/x ֆունկցիայի գրաֆիկը (այստեղ k=−1):

Ցանկացած y=−f(x) ֆունկցիայի գրաֆիկը համաչափ է y=f(x) ֆունկցիայի գրաֆիկին x-երի առանցքի նկատմամբ: Մասնավորապես, y=−1/x ֆունկցիայի գրաֆիկը համաչափ է y=1/x ֆունկցիայի գրաֆիկին x -երի առանցքի նկատմամբ: Ստանում ենք հիպերբոլ, որի ճյուղերը գտնվում են երկրորդ և չորրորդ քառորդներում:

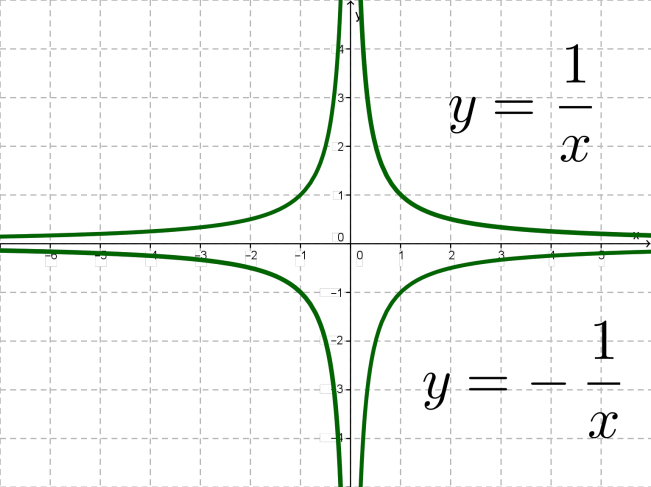
Ընդհանուր դեպքում՝  y=kx, k≠0 ֆունկցիայի գրաֆիկը հիպերբոլ է:

1) Եթե k>0, ապա նրա ճյուղերը գտնվում են առաջին և երրորդ քառորդներում:

2) Եթե k<0, ապա նրա ճյուղերը գտնվում են երկրորդ և չորրորդ քառորդներում:

3) (0;0) կետը հիպերբոլի համաչափության կենտրոնն է: 

4) y=x և y=−x ուղիղները հիպերբոլի համաչափության առանցքներն են: 

5) x-երի և y-երի առանցքները հիպերբոլի ասիմպտոտներն են:  

Սովորաբար ասում են, որ x և y մեծությունները հակադարձ համեմատական են, եթե xy=k (որտեղ k -ն 0 -ից տարբեր թիվ է), կամ որ համարժեք է՝ y=k/x

Այս պատճառով  y=k/x ֆունկցիան երբեմն անվանում են հակադարձ համեմատականության ֆունկցիա (ինչպես y=kx  -ը՝ ուղիղ համեմատականության ֆունկցիա):

k թիվն անվանում են հակադարձ համեմատականության գործակից:

y=k/x ֆունկցիայի հատկությունները։

1. Ֆունկցիան որոշված է ցանկացած կետում, բացի x=0 կետից՝ D=(−∞;0)∪(0;+∞)

2. Եթե x>0, ապա y>0: Եթե x<0, ապա y<0

3. Ֆունկցիան նվազում է (−∞;0) և (0;+∞) միջակայքերի վրա:

4. Ֆունկցիան ոչ վերևից, ոչ էլ ներքևից սահմանափակ չէ:

5. Ֆունկցիան չունի ոչ մեծագույն, ոչ էլ փոքրագույն արժեքներ:

6. Ֆունկցիան անընդհատ է (−∞;0) և (0;+∞) միջակայքերում, իսկ x=0 կետում խզվում է:

Առաջադրանքներ։

1․Գրել  y=5/x ֆունկցիայի հակադարձ համեմատականության գործակիցը: 5

2․Ո՞ր քառորդներում է գտնվում y=−95/x ֆունկցիայի գրաֆիկը:

ա) 2-րդ և 3 -րդ քառորդներում բ) 2-րդ և 4 -րդ քառորդներում

գ) 1-ին և 5 -րդ քառորդներում դ) 1-ին և 4 -րդ քառորդներում

3․ Կառուցել y=4/x ֆունկցիայի գրաֆիկը: Գրաֆիկի օգնությամբ  գտնել. ա) y-ի արժեքը, եթե x=1 բ) x-ի արժեքը, եթե y=−2

Ա=1 x=4

y=-2 x=1/2

4․ Ո՞ր ֆունկցիայի գրաֆիկն է հիպերբոլը:

ա) y=−3x բ) y=4x² գ) y=−4/x դ) ոչ մեկի ե) y=(−x+1)/4

5․ Տրված է y=15/x ֆունկցիան: Գտնել y -ը, եթե x=3

5

6․ a-ի ո՞ր արժեքի դեպքում է (a;−1) կետը պատկանում  y=2/x  ֆունկցիայի գրաֆիկին: 

a=-2

7․ Հայտնի է, որ y=a/x հիպերբոլն անցնում է (8;7) կետով: Գտնել a-ն:

a=56

8․ Արդյո՞ք  B(9;−17) կետը պատկանում է y=153/x ֆունկցիայի գրաֆիկին:

ոչ