Հանրահաշիվ 42

Թեմա՝ y=x² ֆունկցիայի հատկությունները և գրաֆիկը։

y=x² ֆունկցիայի գրաֆիկը պարաբոլն է՝

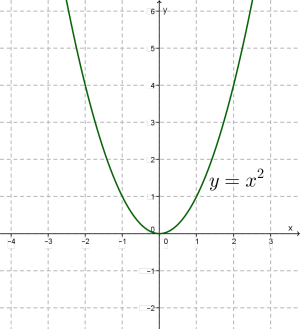
Դիտարկենք գրաֆիկից բխող պարաբոլի որոշ հատկություններ:

1. oy առանցքը հանդիսանում է y=x² պարաբոլի համաչափության առանցք: Համաչափության առանցքը պարաբոլը բաժանում է երկու մասի, որոնք անվանում են պարաբոլի ճյուղեր:
2. Համաչափության oy առանցքը պարաբոլը հատում է որոշակի կետում: Դա այն կետն է, որտեղ միանում են պարաբոլի երկու ճյուղերը: Այն անվանում են պարաբոլի գագաթ:

y=x² պարաբոլը շոշափում է x-երի առանցքը (0;0) կետում:

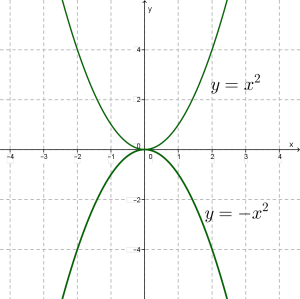
Եթե նույն կոորդինատային համակարգում կառուցենք  y=x² և y=−x² ֆունկցիաների գրաֆիկները, ապա կնկատենք, որ այդ պարաբոլները համաչափ են իրար x-երի առանցքի նկատմամբ: Դա լավ երևում է ներքևի նկարում:

y=kx² ֆունկցիայի հատկությունները k=1 դեպքում

Ֆունկցիայի հատկությունները նկարագրելիս հիմնվենք նրա գրաֆիկի վրա:

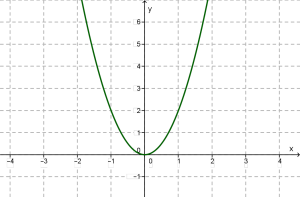
1. y=kx² ֆունկցիան որոշված է x -ի ցանկացած արժեքի համար, այսինքն՝ ֆունկցիայի որոշման տիրույթը ամբողջ (−∞;+∞) թվային առանցքն է:

2. y=0, եթե x=0 և у>0, եթե x≠0: Դա երևում է գրաֆիկից:

3. y=kx² ֆունկցիան աճում է, եթե x≥0 և նվազում է, եթե x≤0

4. Եթե x-ը անսահման տարածվում է դեպի աջ կամ դեպի ձախ (դրական կամ բացասական մնալով), ապա y=kx2 ֆունկցիայի արժեքները դրական մնալով՝ անսահման մեծանում են:

5. y=kx² ֆունկցիայի փոքրագույն արժեքը զրոն է՝ y_min=0, ֆունկցիան այդ արժեքը ընդունում է х=0 դեպքում: Մեծագույն արժեք ֆունկցիան չունի:  

6. y=kx² ֆունկցիան անընդհատ է, քանի որ նրա գրաֆիկը անընդհատ կոր է, որը կարելի է գծել՝ առանց մատիտը թղթից կտրելու:

7. y=kx² (k>0) ֆունկցիան սահմանափակ է ներքևից և սահմանափակ չէ վերևից:

8. y=kx²(k>0) ֆունկցիայի արժեքների բազմությունը [0;+∞) ճառագայթն է:

y=kx² ֆունկցիայի հատկությունները k=-1 դեպքում

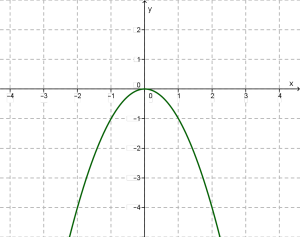
1. y=kx² ֆունկցիայի որոշման տիրույթը ամբողջ (−∞;+∞) թվային առանցքն է:

2. y=0, եթե x=0 և у<0, եթե x≠0:

3. y=kx² ֆունկցիան նվազում է, եթե x≥0 և աճում է, եթե x≤0

4. Եթե x-ը անսահման տարածվում է դեպի աջ կամ դեպի ձախ (դրական կամ բացասական մնալով), ապա y=kx² ֆունկցիայի արժեքները բացասական մնալով՝ անսահման մեծանում են մոդուլով:

5. y=kx² ֆունկցիայի մեծագույն արժեքը զրոն է՝ y _min=0, ֆունկցիան այդ արժեքը ընդունում է х=0 դեպքում: Ֆունկցիան փոքրագույն արժեք  չունի:  

6. y=kx² ֆունկցիան անընդհատ է, նրա գրաֆիկը անընդհատ կոր է, որը կարելի է գծել՝ առանց մատիտը թղթից կտրելու:

7. y=kx² (k<0) ֆունկցիան սահմանափակ է վերևից և սահմանափակ չէ ներքևից:

8. y=kx²(k<0) ֆունկցիայի արժեքների բազմությունը (−∞;0] ճառագայթն է:

Առաջադրանքներ։

1․Որոշել y=x² պարաբոլի ճյուղերի ուղղվածությունը:  

• Ճյուղերն ուղղված են դեպի վերև
• Ճյուղերն ուղղված են դեպի ներքև

2․Գտիր y=x² ֆունկցիայի արժեքների բազմությունը: Ընտրել ճիշտ տարբերակը:

• Ֆունկցիան սահմանափակ չէ ներքևից
• Ֆունկցիան սահմանափակ չէ վերևից

3. Տրված է y=−x² ֆունկցիան: Ընտրել ճիշտ պատասխանը:

ա) y_max=−1 բ) y_max=1 գ) y_max=0

4. Տրված է f(x)=−x² ֆունկցիան: Հաշվել  f(−1); f(−5); f(0); f(2); f(4)։

f(-1)=-1

f(-5)=-25

f(0)=0

f(2)=4

f(4)=16

5. Արդյո՞ք  A(3; 8) կետը պատկանում է  y=x²  ֆունկցիայի գրաֆիկին:

ա) չի պատկանում բ) պատկանում է

6. Արդյո՞ք  A(x; y) կետը պատկանում է  y=x² ֆունկցիայի գրաֆիկին, եթե ա) x=1,y=2; բ) x=3, y=9 գ) x=-2; y=4, դ) x=0,4; y=1,6

ա) x=1,y=2; ոչ
բ) x=3, y=9 այո
գ) x=-2; y=4, այո
դ) x=0,4; y=1,6 ոչ

7. Համեմատել թվային արտահայտությունների արժեքները՝ ա) 1,17² < 1,18² բ) 2,31² < 2․33²

8. y=x²  ֆունկցիայի հանար համեմատել y₁ և y₂ , եթե ա) x₁=0,5 x₂=0,6 բ) x₁=9,2 x₂=8,5

ա) x₁=0,5 y₁=0,25
x₂=0,6 y₂=0,36
y₁<y₂
բ) x₁=9,2 y₁=84,64
x₂=8,5 y₂=72,25
y₁>y₂