Թեմա՝ Մեկ անհայտով գծային անհավասարումների համակարգեր:
Անհավասարումների համակարգը բաղկացած է մեկ կամ մի քանի անհավասարումներից: Այդ անհավասարումները միավորվում են ձևավոր փակագծով: Պետք է գտնել այդ անհավասարումների բոլոր ընդհանուր լուծումները:
Փոփոխականի այն արժեքները, որոնց դեպքում համակարգի անհավասարումներից յուրաքանչյուրը վերածվում է ճիշտ անհավասարության, կոչվում են անհավասարությունների համակարգի լուծումներ:
Գծային անհավասարումների համակարգը լուծելու համար, պետք է լուծել համակարգի յուրաքանչյուր անհավասարումը և այնուհետև գտնել ստացված լուծումների բազմությունների ընդհանուր մասը (հատումը): Դա էլ հենց կլինի համակարգի բոլոր լուծումների բազմությունը:
Լուծել համակարգը՝ նշանակում է գտնել նրա բոլոր լուծումները:
Օրինակ․
Լուծենք հետևյալ համակարգը՝

1. Լուծելով առաջին անհավասարումը, ստանում ենք՝
2x>4
x>2
2. Լուծելով երկրորդ անհավասարումը, ստանում ենք՝
3x<13
x<13/3
3. Ստացված միջակայքերը նշենք թվային առանցքի վրա: Յուրաքանչյուրի համար ընտրենք իր նշումը:

4. Անհավասարումների համակարգի լուծումը թվային առանցքի վրա նշված երկու բազմությունների հատումն է:
Մեր դեպքում ստանում ենք այս պատասխանը՝ (2;13/3)
Առաջադրանքներ․
1. Կոորդինատային ուղղի վրա նշեք անհավասարումների համակարգի բոլոր լուծումները (եթե դրանք գոյություն ունեն)․
ա)
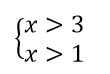
x(3;∞)
բ)

x(1;∞)
գ)

x(2;-∞)
դ)

x(-5;-∞)
ե)

x(-7;-5)
զ)
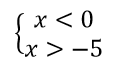
x(-5;0)
2․Փակագծերում նշված թիվը հանդիսանո՞ւմ է արդյոք անհավասարումների համակարգի լուծում՝
ա)
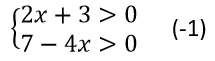
Այո։
բ)
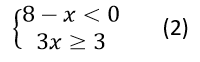
Ոչ։
3․Լուծել անհավասարումների համակարգը

ա) x ∈ (3; -∞);
բ) x ∈ (0; ∞);
գ) x ∈ (-12; 15/4);
դ) x ∈ (−∞, 1/2);
ե) x ∈ (4; ∞);
զ) x ∈ (-∞; 5/3);
է) x ∈ (14/5; ∞);
ը) x ∈ (-∞; -1);
4․Լուծել անհավասարումների համակարգը․
ա)

x ∈ (0.8; ∞);
բ)

x ∈ [2; 4);
գ)

x ∈ (1/5; 1/3);
դ)

x ∈ (0.1; 0.2);
5․Լուծել անհավասարումների համակարգը
ա)

x ∈ [-11; 3);
բ)

x ∈ [4/7; 1);
գ)

x ∈ (-3/2; 0];
դ)
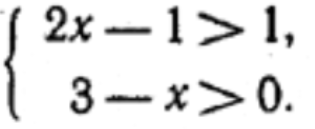
x ∈ (1; 3);
ե)

x ∈ [2; 3);
զ)

x ∈ [2; 3);