Երկու անհայտով երկու գծային հավասարումների համակարգերի լուծման գրաֆիկական եղանակը։

Թեմա՝ Երկու անհայտով երկու գծային հավասարումների համակարգերի լուծման գրաֆիկական եղանակը։

Դիցուք տրված է x և y անհայտներով գծային հավասարումների համակարգ՝

{a₁x+b₁y+c₁=0 a₂x+b₂y+c₂=0

(x;y) թվազույգը կոչվում է համակարգի լուծում, եթե այն բավարարում է համակարգի հավասարումներից յուրաքանչյուրին:

Առաջին աստիճանի գծային հավասարմանը բավարարում են նրա գրաֆիկի՝ ուղիղ գծի վրա գտնվող բոլոր (x;y) կետերը:

Հետևաբար, եթե մենք ուզում ենք, որ բավարարվեն համակարգի երկու գծային հավասարումները միաժամանակ, ուրեմն պետք է փնտրել այնպիսի (x;y) կետեր, որոնք միաժամանակ պատկանում են երկու ուղիղներից յուրաքանչյուրին:

Ուշադրություն

Այսպիսով, համակարգի լուծումները համակարգի հավասարումներով տրվող ուղիղների (գրաֆիկների) ընդհանուր կետերն են:

Օրինակ

1. Լուծենք հետևյալ համակարգը:

{x+2y−5=0, 2x+4y+3=0

x+2y−5=0 հավասարման գրաֆիկն ուղիղ գիծ է: Կառուցենք այդ ուղիղը:  

Գտնենք այս հավասարմանը բավարարող երկու կետ՝

x	5	0
y	0	2,5

xОy հարթության վրա կառուցենք գտնված (5;0) և (0;2.5) կետերը և դրանցով տանենք l1 ուղիղը:

2x+4y+3=0 հավասարման գրաֆիկը ևս ուղիղ գիծ է: 

Գտնենք այս հավասարմանը բավարարող երկու կետ՝

x	−1,5	2,5
y	0	−2

xОy հարթության վրա կառուցենք գտնված (−1.5;0) և (2.5;−2) կետերը և դրանցով տանենք l2 ուղիղը:

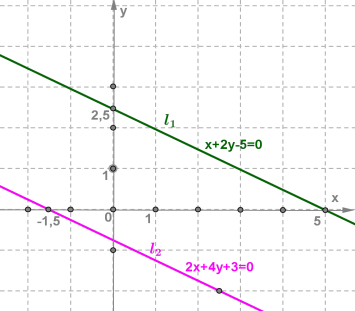
l1 և l2 ուղիղները զուգահեռ են և չունեն ընդհանուր կետեր:

Պատասխան՝ համակարգը լուծում չունի:   

Օրինակ

2. Լուծենք հետևյալ համակարգը:

{2x−y−5=0,2x+y−7=0

Համակարգի հավասարումները բերենք գծային ֆունկցիայի ընդհանուր տեսքին՝ y=2x−5 և y=−2x+7

y=2x−5 ֆունկցիայի գրաֆիկը ուղիղ գիծ է:

Գտնենք այս հավասարմանը բավարարող երկու կետ՝

x	0	3
y	−5	1

xОy հարթության վրա կառուցենք գտնված (0;−5) և (3;1) կետերը և դրանցով տանենք l1 ուղիղը:

y=−2x+7 ֆունկցիայի գրաֆիկը ուղիղ գիծ է:

Գտնենք այս հավասարմանը բավարարող երկու կետ՝

x	0	1
y	7	5

xОy հարթության վրա կառուցենք գտնված (0;7) և (1;5) կետերը և դրանցով տանենք l2 ուղիղը:

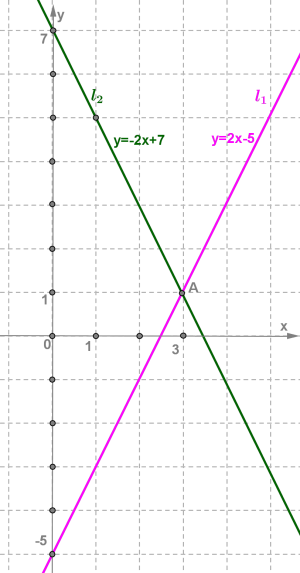
l1 և l2 ուղիղները հատվում են A կետում, որի կոորդինատները համակարգի միակ լուծումն են:

Պատասխան՝ (3;1)

Օրինակներում կիրառեցինք համակարգերի լուծման գրաֆիկական եղանակը:

Գրաֆիկական եղանակը հուսալի չէ, քանի որ միշտ չի հաջողվում ճշգրիտ գտնել հատման կետի կոորդինատները: Այդ պատճառով, խորհուրդ է տրվում գրաֆիկորեն գտնված կետը տեղադրել համակարգի հավասարումների մեջ և համոզվել, որ դրանք բավարարվում են:

Այսպիսով, գալիս ենք հետևյալ եզրակացություններին:Գծային հավասարումների համակարգը գրաֆիկական եղանակով լուծելու համար անհրաժեշտ է՝

1. յուրաքանչյուր հավասարումը լուծել y-ի նկատմամբ,
2. կոորդինատային հարթության վրա կառուցել ստացված հավասարումներին համապատասխանող ուղիղները:

ա Եթե ուղիղները հատվում են, ապա նրանց հատման կետի կոորդինատներից բաղկացած թվազույգը կլինի համակարգի միակ լուծումը:

բ Եթե ուղիղները զուգահեռ լինեն, ապա համակարգը լուծում չունի:

գ Եթե ուղիղները համընկնեն, ապա համակարգն ունի անթիվ բազմությամբ լուծումներ՝ այդ ուղղին պատկանող բոլոր կետերի կոորդինատների թվազույգերը:

1․ Որոշել ֆունկցիայի գրաֆիկի և կոորդինատային առանցքների հատման կետերի կոորդինատաները.

ա) y=2x-7=0

0y -x=0 y=-7

0x -y=0 x=3,5

0y- (0:7)

0x- (35:0)