Category: Մաթեմատիկա
Մաթեմատիկա բազմապատկում քառանիշ թվով 11.10.2021
մաթեմատիկա 07.10.2021
Մաթմատիկա 29.09.2021
Բաժանելի։ բաժանարար= թերի քանորդ(մնացորդ)
Բաժանելի=բաժանարար* թերի քանորդ+մնացորդ
Օրինակ՝ 17։5=3(2 մն․), 17-ը բաժանելին է, 5-ը՝ բաժանարարը, 3-ը՝ թերի քանորդը, իսկ 2-ը՝ մնացորդը։
Բաժանելին՝ 17=5*3+2
Բաժանարար՝ 5=(17-2):3
Առաջադրանքներ
1)Գտեք բաժանելին, եթե բաժանարարը 10 է, թերի քանորդը՝ 7,
մնացորդը՝ 4։ Պատ.՝՝ 74
74= 10*7+4
2)Գտեք բաժանելին, եթե բաժանարարը 21 է, թերի քանորդը՝ 5,
մնացորդը՝ 11։ Պատ.՝ 116
116= 5*21+11
3)Գտեք բաժանելին, եթե բաժանարարը 17 է, թերի քանորդը՝ 2,
մնացորդը՝ 5։ Պատ.՝ 39
17*2+5=39
4)Գտեք բաժանելին, եթե բաժանարարը 101 է, թերի քանորդը՝ 7,
մնացորդը՝ 2։Պատ.՝ 709
101*7+2=709
5) Գտեք բաժանելին, եթե բաժանարարը 53 է, թերի քանորդը՝ 3,
մնացորդը՝ 25։Պատ.՝ 184
53*3+25=184
6) Ի՞նչ ամենամեծ մնացորդ կարող է ստացվել բնական թիվը
5-ի բաժանելիս։ 29:5=5, (4մնացորդ)
7)Ի՞նչ ամենամեծ մնացորդ կարող է ստացվել բնական թիվը
19-ի բաժանելիս։ 37:19=1, (18մնացորդ)
8)Գտեք բաժանարարը, եթե բաժանելին 33 է, թերի քանորդը՝ 5,
մնացորդը՝ 3։ Պատ.՝ 168
9)Գտեք բաժանարարը, եթե բաժանելին 47 է, թերի քանորդը՝ 7,
մնացորդը՝ 5։ Պատ.՝344
10)Գտիր այն ամենափոքր թիվը, որը բաժանվում է 5-ի և 10-ի։Պատ.՝ 10
11)Գտիր այն ամենափոքր թիվը, որը 5-ի և 10-ի բաժանելիս ստանում ենք 2 մնացորդ։ Պատ.՝ 12
12)Գտիր այն ամենափոքր թիվը, որը բաժանվում է 9-ի և 6-ի։ Պատ.՝ 18
13)Գտիր այն ամենափոքր թիվը, որը 9-ի և 6-ի բաժանելիս ստանում ենք 4 մնացորդ։ Պատ.՝ 22
14)Սիրելի սովորողներ, այժմ ինքներդ կազմեք նմանատիպ առաջադրանքներ։
Գտիր այն ամենափոքր թիվը, որը բաժանվում է 10-ի և 9-ի:
Գտեք բաժանելին, եթե բաժանարարը 79 է, թերի քանորդը՝ 46,
մնացորդը՝ 19։ Պատ.՝
Մաթեմատիկա 28. 09.2021
Օրվա գործունեություն․
Հարցերի պարզաբանում
Մտքի վարժանք(բանավոր հաշվարկներ)
Օգտվելով թվերի բաժանելիության հայտանիշներից պատասխանեք հետևյալ հարցերին․
1․ Աստղանիշի ի՞նչ արժեքների դեպքում 689759280 թիվը առանց
մնացորդի կբաժանվի 4-ի։
2. Աստղանիշի ի՞նչ արժեքների դեպքում 59412 թիվը առանց մնացորդի
կբաժանվի 3-ի։
3. Աստղանիշի ի՞նչ արժեքների դեպքում 43128 թիվը առանց մնացորդի
կբաժանվի 9-ի։
4. Աստղանիշի ի՞նչ արժեքների դեպքում 891525 թիվը առանց
մնացորդի կբաժանվի 5-ի
5․Աստղանիշի ի՞նչ արժեքների դեպքում 7009101524 թիվը առանց
մնացորդի կբաժանվի 2-ի։
6․Աստղանիշի ի՞նչ արժեքների դեպքում 800012520 թիվը առանց
մնացորդի կբաժանվի 10-ի։
7․ Աստղանիշների ի՞նչ արժեքների դեպքում 6897592844 թիվը առանց
մնացորդի կբաժանվի 4-ի։
8. Աստղանիշների ի՞նչ արժեքների դեպքում 10755 թիվը առանց մնացորդի
կբաժանվի 3-ի։
9. Աստղանիշների ի՞նչ արժեքների դեպքում 35550 թիվը առանց մնացորդի
կբաժանվի 9-ի։
10. Աստղանիշների ի՞նչ արժեքների դեպքում 18969525 թիվը առանց
մնացորդի կբաժանվի 5-ի
11․Աստղանիշների ի՞նչ արժեքների դեպքում 70097101528 թիվը առանց
մնացորդի կբաժանվի 2-ի։
12․Աստղանիշների ի՞նչ արժեքների դեպքում 8000152520 թիվը առանց
մնացորդի կբաժանվի 10-ի։
13.Սիրելի սովորողներ, այժմ ինքներդ կազմեք նմանատիպ առաջադրանքներ։
Աստղանիշների ի՞նչ արժեքների դեպքում 36* թիվը առանց
մնացորդի կբաժանվի 3-ի։
Աստղանիշների ի՞նչ արժեքների դեպքում 7854* թիվը առանց
մնացորդի կբաժանվի 6-ի։
Աստղանիշների ի՞նչ արժեքների դեպքում 9* թիվը առանց
մնացորդի կբաժանվի 7-ի։
Աստղանիշների ի՞նչ արժեքների դեպքում 10000000000000* թիվը առանց
մնացորդի կբաժանվի 2-ի:
Աստղանիշների ի՞նչ արժեքների դեպքում 14253* թիվը առանց
մնացորդի կբաժանվի 3-ի:
14. Սիրելի սովորողներ, այժմ ինքներդ փնտրեք ու առաջարկեք նոր հայտանիշներ:
Գտեք 11-ի հայտանիշը
Գտեք 2-ի հայտանիշը
Գտեք 9-ի հայտանիշը
Գտեք 3-ի հայտանիշը
Գտեք 8-ի հայտանիշը
մաթեմատիկա 27.09.2021
- 1000000, 3685, 428883, 2560, 785555554 թվերից առանձնացրեք նրանք, որոնք բաժանվում են 5-ի։ 1000000, 3685, 2560:
- 2052, 12557, 1470, 256403 թվերից առանձնացրեք նրանք, որոնք բաժանվում են 2-ի։ 2052, 1470:
- 100000000000000000, 25008, 15760, 154062 թվերից առանձնացրեք նրանք, որոնք բաժանվում են 10-ի։ 10000000000000, 15760:
- 10006, 400005, 100, 1224, 400004 թվերից առանձնացրեք նրանք, որոնք բաժանվում են 3-ի։ 400005, 1224:
- 3033, 12004, 1972, 829, 1020006 թվերից առանձնացրեք նրանք, որոնք բաժանվում են 9-ի։3033, 1020006:
- 220000, 1004, 1051, 2000924, 5011062 թվերից առանձնացրեք նրանք, որոնք բաժանվում են 4-ի։ 220000, 1004, 2000924:
- Օգտագործելով բաշխական օրնեքը ՝ հաշվե՛ք առավել հարմար եղանակով․
106‧58-106‧48=1060
104·25+104·35+104·40= 10800
8. Օգտագործելով բաժանման հատկությունները՝ հաշվե՛ք առավել հարմար եղանակով․
(250+4500):50=95
(490·200):70=1400
9.Հաշվեք արտահայտության արժեքը կիրառելով բաշխական օրնեքը․
60‧(12+38)=3000
10.Աստղանիշը փոխարինիր թվանշաններով այնպես, որ ստացված թիվը բաժանվի 3-ի․
3000018
11. Աստղանիշը փոխարինիր թվանշաններով այնպես, որ ստացված թիվը բաժանվի 9-ի․
40221
մաթեմատիկա 25.09.2021
Հարցերի պարզաբանում
Մտքի վարժանք(բանավոր հաշվարկներ)
Թեմա՝ Թվի բաժանելիության հայտանիշները
Թվի բաժանելիությունը 2-ի
Թիվը բաժանվում է 2-ի, եթե նրա միավորների կարգում գրված թիվը զույգ է, կամ զրո է։ Օրինակներ՝ Առանց բաժանման հաշվեկանոնից օգտվելու կարող ենք ասել, որ 46 և 102 թվերը բաժանվում են 2-ի, քանի որ նրանց միավորների կարգում գրված թիվը զույգ է, 100-ը նույնպես բաժանվում է 2-ի, քանի որ նրա միավորների կարգում գրված թիվը 0 է։ Ստուգում՝ 46։2=23 102։2=51, 100։2=50։
Թվի բաժանելիությունը 5-ի
5-ի բաժանվում է այն թիվը, որի գրառումը վերջանում է 0-ով կամ 5-ով։
Օրինակներ՝ Առանց բաժանման հաշվեկանոնից օգտվելու կարող ենք ասել, որ 105, 165 թվերը բաժանվում են 5-ի, քանի որ նրանց գրառումը վերջանում են 5-ով։ Ստուգում՝ 105։5=21, 165։5=33 100-ը բաժանվում են 5-ի, քանի որ նրա գրառումը վերջանում է 0-ով։ Ստուգում՝ 100։5=20
Թվի բաժանելիությունը 10-ի
10-ի բաժանվում է այն թիվը, որի գրառումը վերջանում է 0-ով։
Օրինակներ՝ 100, 200, 250 թվերը բաժանվում են 10-ի, քանի որ նրանց գրառումը վերջանում են 0-ով։ Ստուգում՝ 100։10=10, 200։10=20, 250։10=25
Թվի բաժանելիությունը 3-ի
Եթե թվի կարգերում եղած թվերի գումարը բաժանվում է 3-ի, ապա թիվը ևս բաժանվում է 3-ի։ Օրինակ՝ Պարզենք 12366 թիվը բաժանվու՞մ է 3-ի։ 1+2+3+6+6=18, 18։3=6, ուստի բաժանվում է։ Ստուգում՝ 12366:3=4122:
Թվի բաժանելիությունը 9-ի
Եթե թվի կարգերում եղած թվերի գումարը բաժանվում է 9-ի, ապա թիվը ևս բաժանվում է 9-ի։ Օրինակ՝ Պարզենք 2277 թիվը բաժանվու՞մ է 9-ի։ 2+2+7+7=18 18։9=2, ուստի բաժանվում է։ Ստուգում՝ 2277:9=253
Թվի բաժանելիությունը 4-ի
Եթե թվի գրառման մեջ վերջին երկու թվանշանները 0-ներ են կամ կազմում են 4-ի բաժանվող թիվ, ապա տրված թիվը բաժանվում է 4-ի։ Օրինակ՝ 2600 թիվը բաժանվում է 4-ի, քանի որ թվի գրառման մեջ վերջին երկու թվանշանները 0-ներ են։
Ստուգում՝ 2600:4=650:
640 թիվը բաժանվում է 4-ի, քանի որ թվի գրառման մեջ վերջին երկու թվանշանները՝ 40-ը, կազմում են 4-ի բաժանվող թիվ, 40։4=10
Ստուգում՝ 640:4=160:
Առաջադրանքներ
1. 126, 805, 1238,30402, 100, 1269,45890,45650 թվերից առանձնացրեք նրանք, որոնք բաժանվում են 3-ի։ 126, 30402, 1269,
2. 333, 124, 1071,8972,829,2398, 10207, 15692 թվերից առանձնացրեք նրանք, որոնք բաժանվում են 9-ի։ 333, 1071,
3. 240, 100000, 1031, 1004, 20015, 28964,63984, 58962 թվերից առանձնացրեք նրանք, որոնք բաժանվում են 4-ի։ 240, 100000, 1004, 28964, 63984
4. 1000, 3685, 4253, 2560, 78954, 45807, 4589, 45865, 4853210 թվերից առանձնացրեք նրանք, որոնք բաժանվում են 5-ի։ 1000, 3685, 2560, 45865, 4853210,
5. 2362, 12059, 147560, 2564057, 125638, 15874, 15463 թվերից առանձնացրեք նրանք, որոնք բաժանվում են 2-ի։ 2362, 147560, 125638, 15874,
6. 100000, 2568, 15760, 154068, 1254000, 1468 թվերից առանձնացրեք նրանք, որոնք բաժանվում են 10-ի։ 100000, 15760, 1254000,
7. Աստղանիշը փոխարինիր թվանշաններով այնպես, որ ստացված թիվը բաժանվի 3-ի․
3189,
4050,
1080,
4116
8. Աստղանիշը փոխարինիր թվանշաններով այնպես, որ ստացված թիվը բաժանվի 9-ի․
7200,
5013,
41238,
32157
9. Աստղանիշը փոխարինիր թվանշաններով այնպես, որ ստացված թիվը բաժանվի 4-ի․
7020,
5000։
10. Աստղանիշը փոխարինիր թվանշաններով այնպես, որ ստացված թիվը բաժանվի 5-ի․
4105,
5115։
Մաթեմատիկա 23.09.2021
Ճամբարականները որոշեցին ժամացույցի թվատախտակը երկու գծով բաժանել երեք մասի այնպես, որ յուրաքանչյուր մասում եղած չորս թվերի գումարները հավասար լինեն: Որո՞նք են ստացված քառյակները, եթե երկնիշ թվերի թվանշանները իրարից բաժանել չի կարելի: Պատ.՝ 13+13=26, 10+3+9+4=26, 5+6+8+7=26, 12+6+8=26,
2․ Արեգը, Դավիթը և Անին ապրում են նույն շենքում։ Դավիթն ապրում է 2 հարկ բարձր, քան Արեգը, բայց 4 հարկ ցածր, քան Անին։ Ով ո՞ր հարկում է ապրում, եթե Արեգն ապրում է այդ շենքի 3֊րդ հարկում։ Պատ.՝ Անի-9 հարկ, Դավիթ-5 հարկ, Արեգ-3,
3. Եթե պապիկը ապրի իր ապրած տարիների կեսը և ևս 1 տարի, ապա կլինի 100 տարեկան։ Քանի՞ տարեկան է պապիկը։ Պատ.՝ հիմա պապիկը 66 տարեկան է:
4․ Շենքի յուրաքանչյուր հարկի բարձրությունը 4մ է։ Այդ շենքի 5֊րդ հարկի հատակին փռված գորգը գետնից ի՞նչ բարձրության վրա է գտնվում։ Պատ.՝ 4*4=16
5․Առավոտյան տողանին 25 ճամբարականներ շարվել էին մեկ շարքով: Յուրաքանչյուր տղայի երկու անմիջական հարևանները աղջիկներ էին: Աղջիկներից ոչ մեկը աղջիկ անմիջական հարևան չուներ: Քանի՞ աղջիկ կար շարքում:Պատ.՝ 13 աղջիկ, 12 տղա,
6․Հասարակածի երկարությունը մոտավորապես 40000կմ է: Հաշվի՛ր, թե քանի՞ անգամ պետք է Նոյեմբերյանից Երևան գնաս, որ այդքան ճանապարհ անցնես, եթե Երևանից Նոյեմբերյան 200կմ է: Պատ.՝ 200 անգամ
7․Գտի՛ր նշված հաջորդականության 5-րդ և 6-րդ անդամների գումարը:
3, 8, 18, 38,68, 108,
8) 89057 թվից ջնջեք երեք թվանշան այնպես, որ ստացված թիվը լինի հնարավորինս մեծ: Պատ.՝ 89
9. Քանի՞ երկնիշ թիվ կա, որի տասնավորի և միավորի գումարը հավասար է ամենափոքր պարզ թվի և ամենափոքր բաղադրյալ թվի գումարին: Պատ.՝ 10, 40, 22, 31,13:
10. Հունիսյան ճամբարի ընթացքում Արևմտյան դպրոցի ճամբարականները կազմակերպեցին ցատկապարկերով վազքի մրցույթ: Արեգը, Դավիթը և Ալենը գրավեցին առաջին երեք տեղերը: Արեգ գրավեց 2-րդ, Ալենը հասավ վերջնագծին Դավթից առաջ: Տղաներից ով ո՞ր տեղը գրավեց: Պատ.՝ Դավիթ-1, Արեգ-2, Ալեն-3,
մաթեմատիկա 22.09
Normal 0 false false false EN-US X-NONE X-NONE Արաբական թվեր 7-րդ դարում նամաշխարհային նոր կրոնի՝ իսլամի տարածման հետևանքով ստեղծվում է նոր աշխարհակալա կայսրություն՝ Արաբական խալիֆայությունը: Նրա խոշոր քաղաքներում, մասնավորապես՝ նորակառույց մայրաքաղաք Բաղդադում, պետության գործիչները ձեռնամուխ են լինում մշակույթի ու գիտությունների զարգացմանը, ի մի բերում մինչ այդ գոյություն ունեցած հնդկական, պարսկական, հունական ու հռոմեական քաղաքակրթությունների նվաճումները։պարսիկ մաթեմատիկոս ալ-Խորեզմի Թվաբանության առաջընթացը կապվում է հնդկական թվերի ներմուծման հետ, որոնք ստեղծվել էին դեռ 5-րդ դարում, և կատարելագործվում 700 թվականին: 628 թվականին հնդիկ մաթեմատիկոս Բրահմագուպտան ստեղծում է նախադեպը չունեցող մի թվանշան՝ 0-ն , որը անհամեմատ հեշտացնելու էր հաշվարկման մեխանիզմը։ Թվերը սկզբում օգտագործվում են ոչ միայն Հնդկաստանում, այլև հարակից Թայլանդում և Հնդկաչին թերակղզու մյուս երկրներում։ Արաբական և հնդարաբական թվերը հնդկական թվերի ձևափոխված տարբերակներն են, որոնք հարմարեցվել էին արաբերենի այբուբենին: «Ալ-ջաբր» բառից առաջանում է «ալգեբրա», իսկ գիտնական ալ-Խորեզմիի անունից՝ «ալգորիթմ» բառերը: Ալ-Խորեզմին հեղինակում է «Հնդկական հաշվարկի մասին» գիրքը, որը վերաբերում էր տասական համակարգին: Այն ընդունվում է ամբողջ խալիֆայության, այդ թվում՝ արաբական Իսպանիայի կողմից։ Արաբական թվերի մասին եվրոպացիները տեղեկանում են 10-րդ դարում։ Պիրենեյան թերակղզու տարածքում Կորդովայի խալիֆայության հարևանությամբ առաջացած մի քանի քրիստոնեադավան պետություններից մեկի՝ Բարսելոնի կոմսության շնորհիվ արաբական թվերը հայտնվում են Իտալիայում: Հռոմի պապ Սիլվեստր II-ը առաջիններից էր, որ ծանոթանում է դրանց, և համոզվում թվերի հարմարության մեջ։ Ալ-Խորեզմիի՝ 825 թվականին գրված աշխատությունը լատիներեն է թարգմանվում միայն 12-րդ դարում՝ որպես Algoritmi de numero Indorum: Դեռ զարգացած միջնադարում, ավելի ստույգ՝ խաչակրաց արշավանքների դարաշրջանում, երբ երբ Եվրոպայում սկսել էր Վերածնունդը, թվերը տարածվում են ամբողջ աշխարհով։ Քանի որ եվրոպացիները թվերին ծանոթացել էին արաբների միջոցով, դրանք անվանում են «արաբական», և ոչ՝ «հնդկական»՝ 0 1 2 3 4 5 6 7 8 9։Հնդկական թվեր Մինչ այդ Եվրոպայում ու Մերձավոր Արևելքում գործածվում էին տարբեր թվաբանական համակարգեր, որոնցից համեմատաբար տարածվածը հռոմեական թվերն էին։ Դրանք իրենցից ներկայացնում էին լատիներենի այբուբենի տառեր, ընդ որում՝ ոչ թե տասը նշան, այլ յոթ՝ I, V, X, L, C, D, M ։ Եթե այս նշանները դրվում էին հաջորդից աջ՝ ապա գումարվում էր VI , իսկ եթե ձախ՝ IV՝ հանվում ։ Հռոմեական թվեր Թվերը գրառելու համար կիրառվում են հռոմեական թվանշաններ` I, V, X, L C, D, M: ռոմեական թվերի համակարգը ոչ դիրքային հաշվարկման համակարգ է։ Թվերը գրվում են թվանշանների կրկնության միջոցով՝ III=3, XX=20 և այլն։ Եթե փոքր արժեքով թվանշանը մեծից հետո է, ապա նրանք գումարվում են, իսկ եթե առաջ է, ապա՝ հանվում՝ VII=5+2=7, CM=-100+1000=900 և այլն։ Տասնորդական հաշվարկման համակարգից հռոմեականի տարբերություններից մեկն այն է, որ տասնորդական համակարգում թվերի մեծացմանը զուգահեռ աճում է դրանք արտահայտող թվանշանների քանակը՝ միանիշ, երկնիշ, եռանիշ և այլն, իսկ հռոմեական համակարգում այդպես չէ։ Օրինակ՝ քառանիշ 2015 թիվը հռոմեական թվանշաններով գրելիս այն ստանում է նույնպես քառանիշ MMXV տեսքը, իսկ ահա նրանից զգալիորեն փոքր 847-ի հռոմեական DCCCXLVII գրառումը բաղկացած է ինը նիշերից։ Եթե տասնորդական համակարգում թվի գրառման ժամանակ գրվում է տասնորդական կարգերն արտահայտող թվերի (տասնավորներ, հարյուրավորներ, հազարավորներ և այլն) միայն առաջին թվերը, ապա հռոմեական համակարգով թվերը գրելու դեպքում դրանք գրվում են ամբողջությամբ, օրինակ՝ 3694=3000+600+90+4=MMMDCXCIV, MMM=3000, DC=600, XC=90, IV=4
5+8-VI=8,
10×10-XII=88,
XX+7-8=19,
Dx10+5000=10000,
XIX+50+51=120,
X+12-12=10,
22+7+XXVIIIII=58,
23+7- XXVIIIII=59,
16+78-LXXX=14,
14+21-XXX=5,
15+14+XI=40,
Normal 0 false false false EN-US X-NONE X-NONE Արաբական թվեր 7-րդ դարում նամաշխարհային նոր կրոնի՝ իսլամի տարածման հետևանքով ստեղծվում է նոր աշխարհակալա կայսրություն՝ Արաբական խալիֆայությունը: Նրա խոշոր քաղաքներում, մասնավորապես՝ նորակառույց մայրաքաղաք Բաղդադում, պետության գործիչները ձեռնամուխ են լինում մշակույթի ու գիտությունների զարգացմանը, ի մի բերում մինչ այդ գոյություն ունեցած հնդկական, պարսկական, հունական ու հռոմեական քաղաքակրթությունների նվաճումները։պարսիկ մաթեմատիկոս ալ-Խորեզմի Թվաբանության առաջընթացը կապվում է հնդկական թվերի ներմուծման հետ, որոնք ստեղծվել էին դեռ 5-րդ դարում, և կատարելագործվում 700 թվականին: 628 թվականին հնդիկ մաթեմատիկոս Բրահմագուպտան ստեղծում է նախադեպը չունեցող մի թվանշան՝ 0-ն , որը անհամեմատ հեշտացնելու էր հաշվարկման մեխանիզմը։ Թվերը սկզբում օգտագործվում են ոչ միայն Հնդկաստանում, այլև հարակից Թայլանդում և Հնդկաչին թերակղզու մյուս երկրներում։ Արաբական և հնդարաբական թվերը հնդկական թվերի ձևափոխված տարբերակներն են, որոնք հարմարեցվել էին արաբերենի այբուբենին: «Ալ-ջաբր» բառից առաջանում է «ալգեբրա», իսկ գիտնական ալ-Խորեզմիի անունից՝ «ալգորիթմ» բառերը: Ալ-Խորեզմին հեղինակում է «Հնդկական հաշվարկի մասին» գիրքը, որը վերաբերում էր տասական համակարգին: Այն ընդունվում է ամբողջ խալիֆայության, այդ թվում՝ արաբական Իսպանիայի կողմից։ Արաբական թվերի մասին եվրոպացիները տեղեկանում են 10-րդ դարում։ Պիրենեյան թերակղզու տարածքում Կորդովայի խալիֆայության հարևանությամբ առաջացած մի քանի քրիստոնեադավան պետություններից մեկի՝ Բարսելոնի կոմսության շնորհիվ արաբական թվերը հայտնվում են Իտալիայում: Հռոմի պապ Սիլվեստր II-ը առաջիններից էր, որ ծանոթանում է դրանց, և համոզվում թվերի հարմարության մեջ։ Ալ-Խորեզմիի՝ 825 թվականին գրված աշխատությունը լատիներեն է թարգմանվում միայն 12-րդ դարում՝ որպես Algoritmi de numero Indorum: Դեռ զարգացած միջնադարում, ավելի ստույգ՝ խաչակրաց արշավանքների դարաշրջանում, երբ երբ Եվրոպայում սկսել էր Վերածնունդը, թվերը տարածվում են ամբողջ աշխարհով։ Քանի որ եվրոպացիները թվերին ծանոթացել էին արաբների միջոցով, դրանք անվանում են «արաբական», և ոչ՝ «հնդկական»՝ 0 1 2 3 4 5 6 7 8 9։Հնդկական թվեր Մինչ այդ Եվրոպայում ու Մերձավոր Արևելքում գործածվում էին տարբեր թվաբանական համակարգեր, որոնցից համեմատաբար տարածվածը հռոմեական թվերն էին։ Դրանք իրենցից ներկայացնում էին լատիներենի այբուբենի տառեր, ընդ որում՝ ոչ թե տասը նշան, այլ յոթ՝ I, V, X, L, C, D, M ։ Եթե այս նշանները դրվում էին հաջորդից աջ՝ ապա գումարվում էր VI , իսկ եթե ձախ՝ IV՝ հանվում ։ Հռոմեական թվեր Թվերը գրառելու համար կիրառվում են հռոմեական թվանշաններ` I, V, X, L C, D, M: ռոմեական թվերի համակարգը ոչ դիրքային հաշվարկման համակարգ է։ Թվերը գրվում են թվանշանների կրկնության միջոցով՝ III=3, XX=20 և այլն։ Եթե փոքր արժեքով թվանշանը մեծից հետո է, ապա նրանք գումարվում են, իսկ եթե առաջ է, ապա՝ հանվում՝ VII=5+2=7, CM=-100+1000=900 և այլն։ Տասնորդական հաշվարկման համակարգից հռոմեականի տարբերություններից մեկն այն է, որ տասնորդական համակարգում թվերի մեծացմանը զուգահեռ աճում է դրանք արտահայտող թվանշանների քանակը՝ միանիշ, երկնիշ, եռանիշ և այլն, իսկ հռոմեական համակարգում այդպես չէ։ Օրինակ՝ քառանիշ 2015 թիվը հռոմեական թվանշաններով գրելիս այն ստանում է նույնպես քառանիշ MMXV տեսքը, իսկ ահա նրանից զգալիորեն փոքր 847-ի հռոմեական DCCCXLVII գրառումը բաղկացած է ինը նիշերից։ Եթե տասնորդական համակարգում թվի գրառման ժամանակ գրվում է տասնորդական կարգերն արտահայտող թվերի (տասնավորներ, հարյուրավորներ, հազարավորներ և այլն) միայն առաջին թվերը, ապա հռոմեական համակարգով թվերը գրելու դեպքում դրանք գրվում են ամբողջությամբ, օրինակ՝ 3694=3000+600+90+4=MMMDCXCIV, MMM=3000, DC=600, XC=90, IV=4
5+8-VI=8,
10×10-XII=88,
XX+7-8=19,
Dx10+5000=10000,
XIX+50+51=120,
X+12-12=10,
22+7+XXVIIIII=58,
23+7- XXVIIIII=59,
16+78-LXXX=14,
14+21-XXX=5,
15+14+XI=40,
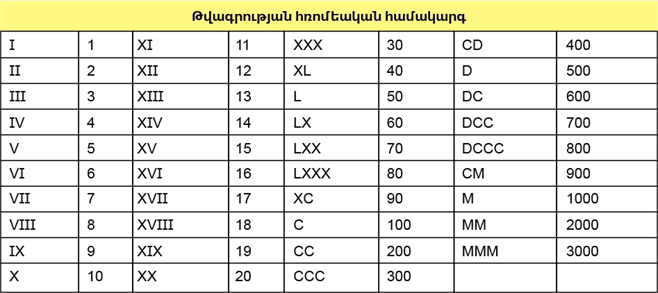
մաթեմատիկա
- Օգտագործելով բաժանման հատկությունները՝ հաշվե՛ք
առավել հարմար եղանակով․
Օրինակ՝ (18+24):6=3+4=7, ( 18։6=3, 24:6=4)
(21+28):7=3+4=7,
21:7=3, 28;7=4
(50+125):25= 50:25=2, 125:25=5, 5+2=7
(24+80):4= 24:4=6, 80:4=20,20+6=26
(16+24):4= 24:4=6, 16:4=4, 4+6=10
(12+18):3= 18:3=6, 12:3=4, 4+6=10
(160+32):4= 32:4=8, 160:4=40, 40+8=48
(455+855):5= 855:5=171, 455:5=91, 91+171=262
(324+664):4= 664:4=166, 324:4= 81, 81+166=247
(182+252):14= 182:14=13, 252:14=18, 18+13= 31
2. Օգտագործելով բաժանման հատկությունները՝ հաշվե՛ք
առավել հարմար եղանակով․
Օրինակ՝ (15·8):5=3·8=24, (15:5=3, 3·8=24)
(288·78):16= 288:16=18, 18*78=1404
(1444·126):18= 126:18=7, 7*1444=10108, 10108*126=1273608
(135·16):15= 135:15=9, 9*16=144
(35·22):11= 22:11=2, 2*35=70,
(6·35):5= 35:5=7, 7*6= 42
(24·130):6= 24:6=4, 4*130= 520
(4011·50):25= 50:25=2, 2*4011=8022
(42·12):7= 42:7=6, 6*12=72