Category: Մաթեմատիկա

Սանդղակներ ու  կոորդինատային ճառագայթ

Սիրելի սովորողներ  սանդղակի ամենապարզ տեսակը ուղղի հատված է, որը գծիկներով բաժանված է հավասար մասերի։ Սանդղակի հարևան գծիկների միջև եղած հատվածը կոչվում է բաժանում։ Մեկ բաժանումը համապատասխանում է չափման ընտրված միավորին։

Դիտարկենք մի ճառագայթ, որը սկիզբ է առնում Օ կետից, և մի հատված, որը կկոչենք միավոր հատված։ Ճառագայթի վրա, Օ կետից սկսած,  հաջորդաբար  նշենք  կետեր այնպես, որ ցանկացած 2 հարևան   կետերի  հեռավորությունը հավասար լինի միավոր հատվածի երկարությանը։

Կոորդինատային ճառագայթ՝

O     1               2    3    4       5      6               7   8     9      10   11 

միավոր հատված

Կետի մոտ գրված թվերին անվանում են կետի կոորդինատներ։ Օրինակ՝ C կետի կոորդինատը հավասար է 5-ի։

C(5)

                 1   2    3     4       5     6   7  8   9       10    11   12

Սիրելի սովորողներ, այսօրվա ձեր աշխատանքը սա   է։

Առաջադրանքներ

1. Ո՞ր  թվերին   են   համապատասխանում   A,B,C,D,E,F    կետերը կոորդինատային ճառագայթի վրա․

A=1

B=5

C=9

D=11

E=12

F=15

• Ի՞ն չ կոորդինատներ ունեն   A և B կետերը ։ Ի՞նչ կոորդինատներ ունեն A և B կետերի միջև նշված կետերը։

A=5

B=10

Միջև  եղած  կետեր՝

1-7

2-9

• A(150) , B(360) և C(30) կետերից ո՞րն է կոորդինատային

ճառագայթի վրա ավելի աջ գտնվում, իսկ ո՞րն է ավելի ձախ գտնվում։

360-գտնվում է  աջ, իսկ  30-ը  ձախ։

• Կոորդինատային ճառագայթի վրա B կետը գտնվում է A(15) կետից ձախ։ Ի՞նչ ամենամեծ կոորդինատ կարող է ունենալ B կետը, իսկ  ի՞նչ ամենափոքր կոորդինատ կարող է ունենալ B կետը։

Ամենամեծ-14

Ամենափոքր-0

• Գծե՛ք Օ կետից սկիզբ առնող կոորդինատային ճառագայթ։ 10մմ երկարություն ունեցող  հատվածը վերցրե ՛ք   որպես միավոր հատված և ճառագայթի վրա նշե՛ք հետևյալ թվերին համապատասխանող կետերը․

ա)0,1,2,3,4,5,6

բ)0,3,6,9

գ)0,2,4,6,8

6․ Գտե՛ք այն 4 թվերը, որոնք գրված պետք է լինեն չափիչ սարքի սանդղակի վրա։

280

0                                                          420

350,70,280, 420,140

• Բերե՛ք  չափիչ  սարքերի  մի քանի  օրինակ և ասե՛ք, թե        չափման ինչ միավորի են համապատասխանում այդ սարքերի սանդղակների բաժանումները։

Մետր-չափում  է  սմ, մետր  և  մմ։

Քանոն-չափում  է  սմ  և մմ։

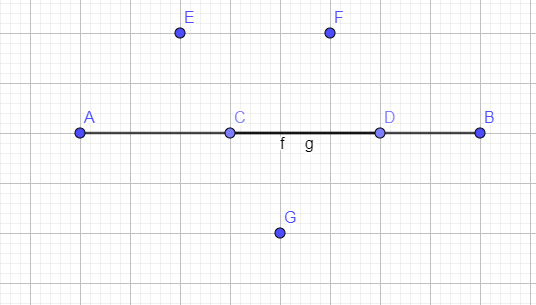
• Գծե՛ք ՕA և ՕB տարբեր ճառագայթներ այնպես, որ ա)դրանք լինեն միևնույն ուղղի ճառագայթներ,

բ) դրանք միևնույն ուղղի ճառագայթներ չլինեն։

• Տրված են 4 կետեր, որոնցից ոչ մի 3-ը չեն գտնվում մի ուղղի վրա։ Յուրաքանչյուր 2 կետով ուղիղ են տարել։ Քանի՞ ուղիղ է տարված։
  
• Գծե՛ք 5սմ երկարությամբ մի AD հատված։ Նրա վրա նշե՛ք այնպիսի B և C կետեր, որ ստացված AB և CD հատվածների համար ունենանք՝

|AB| =2սմ և |CD|=3սմ։

Հավելյալ առաջադրանքներ.

1. Քանի՞ բաժանարար ունի 40-ը։Պատ.՝ 8
2. Քանի՞ բաժանարար ունի 32-ը։Պատ.՝ 5
3. Քանի՞ բաժանարար ունի 12-ը։Պատ՝. 6
4. Քանի՞ բաժանարար ունի 24-ը։Պատ.՝ 8
5. Գտիր 34 թվի ամենամեծ ու ամենափոքր բաժանարարների գումարը։Պատ.՝ 34+1+34=69
6. Գտիր 65 թվի ամենամեծ ու ամենափոքր բաժանարարների գումարը։Պատ.՝ 65+1+65=131

Հատված, նրա երկարությունը,  ճառագայթ, ուղիղ, հարթություն

Եթե մեզ հետաքրքրում է միայն առարկայի երկարությունը, ապա այն կարելի է պատկերել հատվածի տեսքով:

• Դրա համար նշենք A և B կետեր, այնուհետև օգտագործելով քանոնը, դրանք միացնող գիծ տանենք: Կստանանք A և B ծայրակետերով հատված: Ասում են AB հատված:

A                                    B

• Հատվածի ծայրակետերը նշանակում են լատիներեն մեծատառերով՝ A,B,C,D,…

• Սովորաբար հատվածի երկարությունը նշանակելու համար օգտագործում են երկու գծիկ:

Օրինակ՝ | AB |=9սմ:

Հատվածի հիմնական հատկությունը՝

• Հատվածի երկարությունը փոքր է նրա ծայրակետերը միացնող ցանկացած ուրիշ գծի երկարությունից:
• Երկու կետերը միացնող հատվածի երկարությունը կոչվում է այդ կետերի հեռավորությունը:

Ճառագայթ– ունի սկիզբ, բայց  չունի վերջ

A

A ճառագայթ

Օրինակ՝ արևի ճառագայթը

Ուղիղ-չունի ո՛չ սկիզբ, ո՛չ էլ վերջ

Օրինակ՝ հորիզոնը

 a                                                                                             

a    ուղիղ

A                                           B

       AB ուղիղ

Հարթ,      սահմաններ    չունեցող   մակերևույթներն   անվանում   են հարթություններ։

Օրինակ՝         անապատը,  ծովի մակերևույթը։

Միևնույն   հարթության վրա գտնվող  2 ուղիղներ կա՛մ հատվում են, կամ ո՛չ։

Միևնույն   հարթության վրա գտնվող  2 ուղիղները, որոնք չեն հատվում, կոչվում են զուգահեռ  ուղիղներ ։

Հատվող  ուղիղներ

զուգահեռ  ուղիղներ

 

Հարթության  վրա  գտնվող   յուրաքանչյուր   պատկեր  կոչվում  է երկրաչափական  պատկեր։

Մաթեմատիկայի  այն  բաժինը,   որն  ուսումնասիրում է երկրաչափական  պատկերները   և  նրանց հատկությունները,    կոչվում   է   երկրաչափություն։

Հարցեր և առաջադրանքներ

1. Գծեք մի AB հատված և նշեք որևէ 3 կետ, որոնք չեն գտնվում այդ հատվածի վրա, և որևէ 2 կետ, որոնք գտնվում են այդ հատվածի վրա: Պատ.՝

Գծեք այնպիսի AB և CD հատվածներ, որոնք բավարարեն հետևյալ պայամաններին`

| AB |=2սմ 4մմ,     | CD |=3սմ 4մմ:

Գտեք AB և CD հատվածների գումարը։ Պատ.՝

• C կետը գտնվում է AB հատվածի վրա: Հայտնի է, որ CB հատվածի երկարությունը  3 անգամ փոքր է հատվածի երկարությունից: Որքա՞ն է հատվածի երկարությունը, եթե | AB |=12 սմ:Պատ.՝ 4

• Գծեք մի հատված, որի երկարությունը 3 սմ-ով մեծ կլինի 4 սմ երկարություն ունեցող հատվածի երկարությունից:

• Գծեք մի հատված, որի երկարությունը 2 անգամ մեծ կլինի 3 սմ երկարություն ունեցող հատվածի երկարությունից:

• Հայտնի է, որ |AB|=4 սմ, |BC|=7 սմ։ Գտեք AC հատվածի երկարությունը։

• Կարո՞ղ են մի կետից սկիզբ առնել միա քանի ճառագայթներ։ Եթե այո, պատկերել դրանք։

1. Քանի՞ հարթ մակերևույթից է կազմված ակվարիումը:
   5
2. Գծե՛ք մի ուղիղ և նրա վրա նշե՛ք որևէ 2 կետ։ Քանի՞
   հատված և քանի՞ ճառագայթ կստացվի։
   
   
   10.Զուգահեռ ուղիղներից մեկի վրա վերցնենք A և B
   կետերը, մյուսի վրա՝ C և D կետերը։ Կարո՞ղ են արդյոք AB և CD
   հատվածները հատվել։
   
   11.Միևնույն կետով տարե՛ք 2 տարբեր ուղիղներ։ Այդ կետում
   սկզբնավորվող քանի՞ ճառագայթ կստացվի
   

Ընդամենը քանի՞ հատված է պատկերված:

Պատ՝․ 6:

Օրվա գործունեություն․

Հարցերի պարզաբանում

Մտքի վարժանք(բանավոր հաշվարկներ)

Կրկնեք բազմապատկման աղյուսակը։

Թեմա՝ մնացորդով բաժանում։

Ոչ բոլոր թվերն են ամբողջությամբ բաժանվում մեկ ուրիշ թվի վրա։ Նման դեպքում բաժանման արդյունքում ստանում ենք թերի քանորդ ու մնացորդ։

Բաժանելի։ բաժանարար=թերի քանորդ(մնացորդ)

Բաժանելի=բաժանարար*թերի քանորդ+մնացորդ

Բաժանարար=(Բաժանելի-մնացորդ)։թերի քանորդ

1)Գտեք բաժանելին, եթե բաժանարարը 15 է, թերի քանորդը՝ 8, մնացորդը՝ 3։

Լուծում՝ 15*8=120, 120+3=123:
2) Գտիր բաժանարարը, եթե բաժանելին 165 է, թերի քանորդը՝ 4,
մնացորդը՝ 1։ Լուծում՝ 165-1=164,164:4=41
3)Գտեք բաժանելին, եթե բաժանարարը 17 է, թերի քանորդը՝ 6,
մնացորդը՝ 3։Լուծում՝ 17*6=102, 102+3=105:
4) Գտիր բաժանարարը, եթե բաժանելին 788 է, թերի քանորդը՝ 3,
մնացորդը՝ 2։ 788-2=786, 786:3=262

5)Գտեք բաժանելին, եթե բաժանարարը 21 է, թերի քանորդը՝ 5,
մնացորդը՝ 4։Լուծում՝ 21*5=105, 105+4=109
6) Գտիր բաժանարարը, եթե բաժանելին 569 է, թերի քանորդը՝ 9,
մնացորդը՝ 2։Լուծում՝ 569-2=567, 567:9=63:

7) Ի՞նչ ամենամեծ մնացորդ կարող է ստացվել բնական թիվը
108-ի բաժանելիս։ Պատ.՝ 107

8)Ի՞նչ ամենամեծ մնացորդ կարող է ստացվել բնական թիվը
5-ի բաժանելիս։Պատ.՝ 4

9)Ի՞նչ ամենամեծ մնացորդ կարող է ստացվել բնական թիվը
36-ի բաժանելիս։Պատ.՝ 35

10) Առանձնացրեք 4-ի բաժանվող թվերը.

2500, 16635, 180012, 3697, 12560, 2504, 1450: 4-ի բաժանվող թվերը 2500, 180012, 12560, 2504,

11)Առանձնացրեք 3-ի բաժանվող թվերը.

1560, 1568, 3609, 15880, 3605, 14500: 3-ի բաժանվող թվերը 1560, 3609:

12)Առանձնացրեք 9-ի բաժանվող թվերը.

3780, 2156, 108819, 1000, 1605 :9-ի բաժանվող թվերը 3780, 108819:

24.11.2021

Օրվա գործունեություն․

Հարցերի պարզաբանում

Մտքի վարժանք(բանավոր հաշվարկներ)

Կրկնեք բազմապատկման աղյուսակը։
Ինքնաստուգում

1)Գտեք բաժանելին, եթե բաժանարարը 21 է, թերի քանորդը՝ 10,
մնացորդը՝ 6։ Լուծում՝ 21*10=210, 210+6=216:
2) Գտիր բաժանարարը, եթե բաժանելին 186 է, թերի քանորդը՝ 5,
մնացորդը՝ 1։ Լուծում՝ 186-1=185, 185:5=37:
3)Գտեք բաժանելին, եթե բաժանարարը 33 է, թերի քանորդը՝ 4,
մնացորդը՝ 3։ Լուծում՝ 33*4=132, 132+3=135:
4) Գտիր բաժանարարը, եթե բաժանելին 126 է, թերի քանորդը՝ 4,
մնացորդը՝ 2։Լուծում՝ 126-2=124, 124:4=31

5)Գտեք բաժանելին, եթե բաժանարարը 17 է, թերի քանորդը՝ 19,
մնացորդը՝ 5։ Լուծում՝ 17*19=323, 323+5=328:
6) Գտիր բաժանարարը, եթե բաժանելին 158 է, թերի քանորդը՝ 3,
մնացորդը՝ 2: Լուծում՝ 158-2=156, 156:3=52:

7) Ի՞նչ ամենամեծ մնացորդ կարող է ստացվել բնական թիվը
3-ի բաժանելիս։Պատ.՝ 2

8)Ի՞նչ ամենամեծ մնացորդ կարող է ստացվել բնական թիվը
25-ի բաժանելիս։ Պատ.՝ 24

9)Ի՞նչ ամենամեծ մնացորդ կարող է ստացվել բնական թիվը
106-ի բաժանելիս։ Պատ.՝ 105

10) Առանձնացրեք 4-ի բաժանվող թվերը.

1000, 1785, 2924, 30261, 2820, 34581, 3565, 2812, 4533:

4-ի բաժանվող թվերը. 1000, 2924, 2820, 2812:

Գտիր 10000 և 5-ի քանորդը՝  10000:5=2000=Ս

Գտիր 10-ի ½ մասը 10։2=5Ե

Գտիր 4-ի ½  մասը 4:2=2Բ
 
Գտիր 4-ի 4/4 մասը 4։4=1=Ա

Գտիր 1000-ի ½ մասը 1000×2=2000=Ս

Գտիր 16000-ի ¼ մասը 16000։4=4000Տ

Գտիր 4-ի 10/10 մասը 10։10=1=Ա

Գտիր 3000-ի և 2-ի արտադրյալը 2×3000=6000Ց

Գտիր 3500-ի և 2-ի արտադրյալը 2×3500=7000Ի
Այս խնդիրները կազմել են

23.11.2021

Օրվա գործունեություն․

Հարցերի պարզաբանում

Մտքի վարժանք(բանավոր հաշվարկներ)

Կրկնեք բազմապատկման աղյուսակը։

Կրկնենք անցածը։

Թեմա՝ մնացորդով բաժանում։

Ոչ բոլոր թվերն են ամբողջությամբ բաժանվում մեկ ուրիշ թվի վրա։ Նման դեպքում բաժանման արդյունքում ստանում ենք թերի քանորդ ու մնացորդ։

Բաժանելի։ բաժանարար=թերի քանորդ(մնացորդ)

Բաժանելի=բաժանարար*թերի քանորդ+մնացորդ

Բաժանարար=(Բաժանելի-մնացորդ)։թերի քանորդ

Օրինակ՝ 17։5=3(2մն․), 17-ը բաժանելին է, 5-ը՝ բաժանարար, 3-ը՝ թերի քանորդ, իսկ 2-ը՝ մնացորդ։

17=5*3+2

5=(17-2):3

Բաժանման արդյունքում ստացված մնացորդը միշտ փոքր է այն բնական թվից, որի վրա թիվը բաժանել ենք։

Օրինակ՝ բնական թիվը 5-ի բաժանելիս կարող ենք ստանալ 1, 2, 3 կամ 4 մնացորդ։

Առաջադրանքներ։

Օրինակներ՝

Գտեք բաժանելին, եթե բաժանարարը 11 է, թերի քանորդը՝ 3,
մնացորդը՝ 2։

11*3+2=35

Գտիր բաժանարարը, եթե բաժանելին 16 է, թերի քանորդը՝ 5,
մնացորդը՝ 1։

(16-1):5=15:5=3

1)Գտեք բաժանելին, եթե բաժանարարը 13 է, թերի քանորդը՝ 6,
մնացորդը՝ 1։ Լուծում՝ 13*6=78, 78+1=79:
2) Գտիր բաժանարարը, եթե բաժանելին 155 է, թերի քանորդը՝ 4,
մնացորդը՝ 3։ Լուծում՝ 155-3=152,152:4=38:
3)Գտեք բաժանելին, եթե բաժանարարը 42 է, թերի քանորդը՝ 6,
մնացորդը՝ 5։ Լուծում՝ 42*6=252, 252+5=257:
4) Գտիր բաժանարարը, եթե բաժանելին 159 է, թերի քանորդը՝ 5,
մնացորդը՝ 4։ Լուծում՝ 159-4=155, 155:5=31:

5)Գտեք բաժանելին, եթե բաժանարարը 18 է, թերի քանորդը՝ 11,
մնացորդը՝ 7։ Լուծում՝ 18*11=198, 198+7=205:
6) Գտիր բաժանարարը, եթե բաժանելին 126 է, թերի քանորդը՝ 11,
մնացորդը՝ 5: Լուծում՝126-5=121, 121:11=11:

7) Ի՞նչ ամենամեծ մնացորդ կարող է ստացվել բնական թիվը
35-ի բաժանելիս։ Պատ.՝ 34

8)Ի՞նչ ամենամեծ մնացորդ կարող է ստացվել բնական թիվը
18-ի բաժանելիս։ Պատ.՝ 17

9)Ի՞նչ ամենամեծ մնացորդ կարող է ստացվել բնական թիվը
101-ի բաժանելիս։Պատ.՝100

10) Սիրելի սովորողներ, այժմ ինքներդ կազմեք նմանատիպ առաջադրանքներ։

Իմ կազմած առաջադրանքները

Գտեք բաժանելին, եթե բաժանարարը 11 է, թերի քանորդը՝ 3,
մնացորդը՝ 2։

11*3+2=35

Գտիր բաժանարարը, եթե բաժանելին 16 է, թերի քանորդը՝ 5,
մնացորդը՝ 1։

(16-1):5=15:5=3

1)Գտեք բաժանելին, եթե բաժանարարը 23 է, թերի քանորդը՝ 5,
մնացորդը՝ 3։

23×5=115

155+3=118

2) Գտիր բաժանարարը, եթե բաժանելին 156 է, թերի քանորդը՝ 8,
մնացորդը՝ 4։

156-4=152

152:8=19

3)Գտեք բաժանելին, եթե բաժանարարը 63 է, թերի քանորդը՝ 9,
մնացորդը՝ 7։

63×9=567

567+7=574

4) Գտիր բաժանարարը, եթե բաժանելին 756 է, թերի քանորդը՝ 11,
մնացորդը՝ 8։

756-8=748

748:11=68

5)Գտեք բաժանելին, եթե բաժանարարը 113 է, թերի քանորդը՝ 12,
մնացորդը՝ 10։

113×12=1356

1356+10=1366

6) Գտիր բաժանարարը, եթե բաժանելին 245 է, թերի քանորդը՝ 11,
մնացորդը՝ 3։

245-3=242

242:11=22

Ի՞նչ ամենամեծ մնացորդ կարող է ստացվել բնական թիվը
67-ի բաժանելիս։ Պատ.՝ 66

Ի՞նչ ամենամեծ մնացորդ կարող է ստացվել բնական թիվը
15-ի բաժանելիս։ Պատ.՝ 14

Թվերը գրելու հնամենի եղանակը

Թվերի գրառումը  հայերենի այբուբենի տառերով․

Ա	Բ	Գ	Դ	Ե	Զ	Է	Ը	Թ
1	2	3	4	5	6	7	8	9
Ժ	Ի	Լ	Խ	Ծ	Կ	Հ	Ձ	Ղ
10	20	30	40	50	60	70	80	90
Ճ	Մ	Յ	Ն	Շ	Ո	Չ	Պ	Ջ
100	200	300	400	500	600	700	800	900
Ռ	Ս	Վ	Տ	Ր	Ց	Ւ	Փ	Ք
1000	2000	3000	4000	5000	6000	7000	8000	9000

Օգտվելով  այս  աղյուսակից  լուծեք  խաչբառը

Խաչբառ

Հարցերը լուծեք   բանավոր և  ներկայացրեք  հայերենի այբուբենի տառերով․

Հորիզոնական

1. Գտեք  բաժանելին, եթե բաժանարարը 33 է, թերի քանորդը՝ 6, մնացորդը՝ 2: Լուծում՝ 33*6+2=200
2. Գտիր բաժանարարը, եթե բաժանելին 323 է, թերի քանորդը՝ 8, մնացորդը՝ 3: Լուծում՝ 323-3=320, 320:8=40:
3. Գտեք   ուղղանկյունանիստի ծավալը, եթե նրա չափումներն են՝  2 սմ, 5 սմ, 2 սմ։ Գրել միայն թվային մասը։  Լուծում՝ 2*5*2=20:
4. Ի՞նչ  ամենամեծ մնացորդ կարող է ստացվել բնական թիվը           10-ի բաժանելիս։ Պատ.՝ 9
5. Ո՞րն է ամենափոքր բնական թիվը։  1
6. Գտեք 25000-ի 1/5 մասը:   Պատ.՝ 5000

Ուղղաձիգ

1. Գտեք   2500-ի  4/5 մասը։ Պատ.՝ 125
2. Գտեք ամենափոքր քառանիշ թվի և ամենամեծ եռանիշ թվի  տարբերության  հնգապատիկը։  Պատ.՝ 5
3. Ո՞րն է ամենափոքր զույգ բնական թիվը։  Պատ.՝ 2
4. Գտեք ամենափոքր հնգանիշ թվի  և  ամենափոքր բնական թվի հնգապատիկի  քանորդը։  Լուծում՝ 10000:5=2000:
5. Ի՞նչ  թիվ է մտապահել Սոնան, եթե նրա մտապահած թիվը փոքրացնենք 4 անգամ, արդյունքից հանենք ամենամեծ եռանիշ թիվը, կստանանք ամենափոքր բնական թիվը։ Պատ.՝ Սոնան մտապահել էր 3996:
6. Ո՞րն է ամենափոքր կենտ բնական թիվը։  Պատ.՝3
7. Որքանո՞վ կմեծանա  եռանիշ թիվը, եթե նրան  ձախից կցագրենք 6  թվանշանը։  396, 6396: Թիվը մեծացավ 6000-ով:
8. Երկու արկղերում կա 30 գնդակ։ Քանի՞  գնդակ կա առաջին արկղում, եթե առաջին արկղից երկրորդի մեջ դնենք 10 գնդակ, իսկ երկրորդից առաջինի մեջ՝ 5 գնդակ, ապա երկու արկղերում հավասար քանակով գնդակներ կլինեն։ Պատ.՝ 20-առաջին երկրորդ-10:

				Ս
				ե
				բ
Մ	խ	ի	թ	ա	ր
				Ս
				տ
				ա
				Ց
				ի

17․11․2021

Օրվա գործունեություն․

Հարցերի պարզաբանում

Մտքի վարժանք(բանավոր հաշվարկներ)

Ինքնաստուգում

1․Հաշվեք ուղղանկյունանիստի մակերևույթի մակերեսը, եթե նրա չափումներն են՝ 6 սմ, 9 սմ,  12 սմ։ Լուծում՝

6*9=54,

6*12=72,

9*12=108,

54*2=108,

72*2=144,

108*2=216,

108+144+216=468:

2.Հաշվեք ուղղանկյունանիստի ծավալը, եթե նրա չափումներն են՝ 7 դմ, 8 դմ,  10 դմ։

Լուծում՝ 7*8*10=560 սմ քառ:

3․Հաշվեք  9 սմ կող ունեցող  խորանադի ծավալը։

Լուծում՝

9*9*9=729 սմ խոր.

Մակերևույթի մակերես

4․ Հաշվեք 8 դմ կող ունեցող խորանադի մակերևույթի մակերեսը։

Լուծում՝

8*8*8=512

Մակերևույթի մակերես

5․ 180, 124, 1025, 25681, 10000, 369   թվերից առանձնացրեք նրանք, որոնք բաժանվում են 5-ի։ 180, 1025, 10000,

6․ 14, 25, 15980, 1546, 23551, 25693   թվերից առանձնացրեք նրանք, որոնք բաժանվում են 2-ի։ 14, 15980, 1546:

7․ 6358, 1500, 3650, 1423, 2544  թվերից առանձնացրեք նրանք, որոնք բաժանվում են 10-ի։ 1500, 3650:

8․ 4501, 3691, 1008, 3702, 2566 թվերից  առանձնացրեք  նրանք, որոնք  բաժանվում են 3-ի։ 1008, 3702:
9․ 909, 1000, 33003, 6009, 60606,  թվերից առանձնացրեք նրանք, որոնք բաժանվում են 9-ի։ 909, 33003,60606:

10․ 3600, 2425, 1800, 1016, 2598 թվերից առանձնացրեք նրանք, որոնք բաժանվում են 4-ի։ 3600, 1800, 1016, 2598:

16․11․2021

Օրվա գործունեություն․

Հարցերի պարզաբանում

Մտքի վարժանք(բանավոր հաշվարկներ)

Թեմա՝ Ուղղանկյունանիստի մակերևույթի մակերես և ծավալ

1․Հաշվեք ուղղանկյունանիստի մակերևույթի մակերեսն ու ծավալը, եթե նրա չափումներն են՝ 2 սմ, 9 սմ,  11 սմ։

Լուծում՝

2*9=18,

2*11=22,

9*11=99,

18*2=36,

22*2=44,

99*2=198,

36+44+198=278,

2*9*11=198:

2․Հաշվեք ուղղանկյունանիստի մակերևույթի մակերեսն ու ծավալը, եթե նրա չափումներն են՝ 5 դմ, 7 դմ,  8 դմ։

Լուծում՝

5*7=35,

5*8=40,

7*8=56,

35*2=70,

40*2=80,

56*2=112,

70+80+112=262:

5*7*8=280:

3․Հաշվեք ուղղանկյունանիստի մակերևույթի մակերեսն ու ծավալը, եթե նրա չափումներն են՝ 6 սմ,  12 սմ, 10 սմ։

Լուծում՝

6*12=72,

6*10=60,

12*10=120,

72*2=144,

60*2=120,

120*2=240,

144+120+240=504,

6*12*10=720:

4․Հաշվեք ուղղանկյունանիստի մակերևույթի մակերեսն ու ծավալը, եթե նրա չափումներն են՝ 13 սմ, 15 սմ,  10 սմ։

Լուծում՝

13*15=195,

13*10=130,

10*15=150,

195*2=390,

130*2=260,

150*2=300,

390+260+300=950,

13*10*15=1950:

5․Հաշվեք ուղղանկյունանիստի մակերևույթի մակերեսն ու ծավալը, եթե նրա չափումներն են՝

Լուծում՝

11 սմ,  12 սմ, 10 սմ։

11*12=132,

11*10=110,

12*10=120,

132*2=264,

110*2=220,

120*2=240,

264+220+240=724:

11*12*10=1320:

6․ Հաշվեք ուղղանկյունանիստի մակերևույթի մակերեսն ու ծավալը, եթե նրա չափումներն են՝     

 3 դմ,  20 սմ, 10 սմ։

Լուծում՝

3*20=60,

3*10=30,

20*10=200,

60*2=120,

30*2=60,

200*2=400,

120+60+400=580:

3*20*10=600:

7․ Հաշվեք ուղղանկյունանիստի մակերևույթի մակերեսն ու ծավալը, եթե նրա չափումներն են՝

11 սմ, 12 սմ, 14 սմ։

Լուծում՝ 11*12=132,

11*14=154,

12*14=168,

132*2=264,

154*2=308,

168*2=336,

264+308+336=908,

11*12*14=1848:

8․ Հաշվեք ուղղանկյունանիստի մակերևույթի մակերեսն ու ծավալը, եթե նրա չափումներն են՝

15 սմ, 16 սմ, 17սմ։

Լուծում՝

15*16=240,

15*17=255,

16*17=272,

240*2=480,

255*2=510,

272*2=544,

480+510+544=1534:

15*16*17=4080:

9․ Հաշվեք ուղղանկյունանիստի մակերևույթի մակերեսն ու ծավալը, եթե նրա չափումներն են՝

10 սմ, 12 սմ, 14 սմ։

Լուծում՝

12*14*10=1680

12*14=168

168*2=336

12*10=120

120*2=240

14*10=140

140*2=280

336+240+280=856

10․ Սիրելի սովորողներ, այժմ ինքներդ կազմեք նմանատիպ խնդիրներ։

1.Հաշվեք ուղղանկյունանիստի մակերևույթի մակերեսն ու ծավալը, եթե նրաչափումներնեն՝

18սմ, 12 սմ, 19սմ։

Օրվա գործունեություն․

Հարցերի պարզաբանում

Մտքի վարժանք(բանավոր հաշվարկներ)

Թեմա՝ Ուղղանկյունանիստի մակերևույթի մակերես

Սիրելի սովորողներ, այսօր կսովորենք հաշվել ուղղանկյունանիստի մակերևույթի մակերեսը, ինչպես նաև կկատարեք գործնական աշխատանք։

Նախ ուսումնասիրենք ուղղանկյունանիստի փռվածքը։ Այն բաղկացած է 6 ուղղանկյուններից։

Օրինակի վրա հասկանանք, թե ինչպես պատրաստենք ուղղանկյունանիստ։ Ընտրեք 3 տարբեր չափումներ, օրինակ՝ 3 սմ, 5 սմ և 8 սմ։ Գունավոր ստվարաթղթից կտրեք 3 սմ և 5 սմ կողմերով 2 հատ ուղղանկյուն, կտրեք նաև 5 սմ և 8 սմ կողմերով 2 հատ ուղղանկյուն, որից հետո կտրեք 3 սմ և 8 սմ կողմերով 2 հատ ուղղանկյուն։ Այժմ սկոչի միջոցով այդ ուղղանկյունները միացրեք այնպես, որ ստանաք ուղղանկյունանիստի փռվածքը, դրանից հետո հեշտությմաբ կստանաք ուղղանկյունանիստ, որի չափումներն են՝ 3 սմ, 5 սմ և 8 սմ։

Ուղղանկյուանանիստի մակերևույթի մակերեսը նրա բոլոր նիստերի(ուղղանկյունների)  մակերերսների գումարն է։

Ուղղանկյունանիստի  չափումներն են՝ ուղղանկյունանիստի լայնությունը, երկարությունը և բարձրությունը։

Եթե ուղղանկյունանիստի չափումները նշանակենք a,b,c, քանի որ ուղղանկյունանիստի հանդիպակաց նիստերը իրար հավասար են, ուստի  նրա բոլոր նիստերի  մակերերսների գումարը կլինի՝ 2*a*b+2*b*c+2*a*c, որն էլ ուղղանկյունանիստի մակերևույթի մակերեսն է։

Օրինակ՝ հաշվենք 3 սմ, 5 սմ և 8 սմ չափումներով ուղղանկյունանիստի մակերևույթի մակերեսը։

a=3 սմ, b=5 սմ, c=8 սմ, ուրեմն ուղղանկյունանիստի մակերևույթի մակերեսը՝ 2*3*5+2*5*8+2*3*8=30+80+48=158 սմ քառ․։

Ավելի լավ հասկանալու համար նախ պատկերենք ուղղանկյունանիստի փռվածքը՝

Նախ նկատենք, որ կա 2 հատ 3 սմ և 5 սմ կողմերով ուղղանկյուն։ Հաշվենք 3 սմ և 5 սմ կողմերով ուղղանկյուններից յուրաքանչյուրի մակերեսը՝ 3*5=15 սմ քառ․։

Այժմ նկատենք, որ կա 2 հատ 3 սմ և 8 սմ կողմերով ուղղանկյուն։ Հաշվենք 3 սմ և 8 սմ կողմերով ուղղանկյուններից յուրաքանչյուրի մակերսը՝ 3*8=24 սմ քառ․:

Այնուհետև նկատենք, որ կա 2 հատ 5 սմ և 8 սմ կողմերով ուղղանկյուն։ Հաշվենք 5 սմ և 8 սմ կողմերով ուղղանկյուններից յուրաքանչյուրի մակերեսը՝ 5*8=40 սմ քառ․։

S(մակերևույթի մակերես)=2*15+2*24+2*40=30+48+80=158 սմ քառ․

Առաջադրանքներ․

1․Հաշվեք ուղղանկյունանիստ մակերևույթի մակերեսը, եթե նրա չափումներն են՝ 5 դմ, 7 դմ,  8 դմ։

Լուծում՝ 5*7=35,7*8=56, 8*5=40,

35*2=70, 56*2=112, 40*2=80,

70+112+80=262

2․Հաշվեք ուղղանկյունանիստ մակերևույթի մակերեսը, եթե նրա չափումներն են՝ 6 սմ,  12 սմ, 10 սմ։

Լուծում՝

6*12=72,

6*10=60,

10*12=120,

72*2=144, 60*2=120, 120*2=240

144+120+240=504

3․Հաշվեք ուղղանկյունանիստ մակերևույթի մակերեսը, եթե նրա չափումներն են՝ 3 սմ, 5 սմ,  10 սմ։Լուծում՝

3*5=15,

3*10=30,

5*10=50,

15*2=30, 30*2=60, 50*2=100:

30+60+100=190

4․Հաշվեք ուղղանկյունանիստ մակերևույթի մակերեսը, եթե նրա չափումներն են՝

11 սմ,  12 սմ, 10 սմ։

Լուծում՝

11*12=132,

11*10=110,

10*12=120,

132*2=264, 110*2=220, 120*2=240:

264+220+240=724:

5․ Հաշվեք ուղղանկյունանիստի մակերևույթի մակերեսը, եթե նրա չափումներն են՝         

 3 դմ,  20 սմ, 10 սմ։

Լուծում՝

3*20=60,

3*10=30,

20*10=200:

60*2=120, 30*2=60, 200*2=400:

120+60+400=580:

6․ Հաշվեք ուղղանկյունանիստ մակերևույթի մակերեսը, եթե նրա չափումներն են՝

11 սմ, 12 սմ, 14 սմ։

Լուծում՝

11*12=132,

11*14=154,

12*14=168,

132*2=264, 154*2=308,168*2=336:

264+308+336=908: