Category: Հանրահաշիվ

Թեմա՝  Թվային միջակայքեր թվային ուղղի վրա։

Գիտենք, որ իրական թվերի երկրաչափական մոդելը թվային ուղիղն է: Ցանկացած իրական թիվ թվային ուղղի վրա ունի իր դիրքը: Հիմա կպարզենք, թե ինչպես են թվային ուղղի վրա պատկերվում թվային միջակայքերը: Կօգտագործենք հետևյալ նշանակումները. 

Անհավասարությունների և ծայրակետերի նշանակումներ	Բազմությունների նշանակումներ
≤ կամ ≥ • (ծայրակետն ընդգրկված է)	[ և] քառակուսի փակագծեր
< կամ > о (ծայրակետն ընդգրկված չէ)	( և ) կլոր փակագծեր

Գոյություն ունեն թվային ուղղի վրա բազմությունների 4 տեսակի նշանակումներ:

Ամբողջ թվային ուղիղը նշանակվում է այսպես՝ (−∞;∞)

Բաց և փակ միջակայքեր թվային առանցքի վրա

Արդեն դիտարկել ենք թվային ուղղի վրա որոշ բազմությունների նշանակումը՝ (−∞; ∞), (a;+∞),[a;+∞),(−∞;a],(−∞;a)

Սրանք, այսպես կոչված, անսահմանափակ բազմություններ (մի կողմից կամ երկու կողմից) են: Դիտարկենք սահմանափակ բազմություններ թվային առանցքի վրա:

Եթե x թիվը միաժամանակ բավարարում է x>−4 և x<5 անհավասարություններին, ապա այն բավարարում է −4<x<5 երկկողմանի անհավասարությանը:

−4<x<5 երկկողմանի անհավասարությանը բավարարող բոլոր թվերի բազմությունը անվանում են թվային միջակայք և նշանակում են այսպես՝ (−4;5):

Միջակայքը պատկերենք թվային ուղղի վրա: Կարդում ենք՝ «−4, 5 ինտերվալ», կամ «բաց միջակայք» : Նկատենք, որ հատվածի ծայրակետերը ընդգրկված չեն (սևացված չեն):

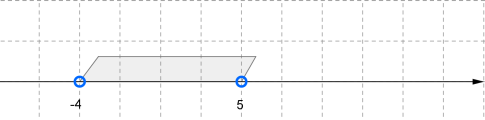
Դիտարկենք ուրիշ միջակայքեր:

−4≤x≤5 կամ x∈[−4;5]: Կարդում ենք՝ «−4, 5 հատված», կամ «փակ միջակայք»: Նկատենք, որ հատվածի ծայրակետերը ընդգրկված են (սևացված են):

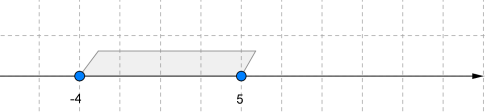
−4≤x<5 կամ x∈[−4;5): Կարդում ենք՝ «−4, 5 կիսաինտերվալ», կամ «կիսաբաց միջակայք»: Նկատենք, որ կիսաինտերվալի ծայրակետերից մեկը՝ −4 -ը ընդգրկված է (սևացված է), իսկ մյուսը՝ 5 -ը ընդգրկված չէ (սևացված չէ):

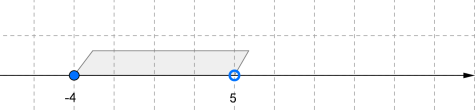
−4<x≤5 կամ x∈(−4;5]: Սա ևս կիսաինտերվալ է՝ բաց ձախ ծայրակետով:

x-երի առանցքի a և b կետերից և նրանց միջև գտնվող բոլոր կետերից բաղկացած բազմությունն անվանում են a-ից b հատված և նշանակում՝ [a;b]:

Հարցեր և առաջադրանքներ:

1. Ո՞ր թվեր են պատկանում տրված միջակայքին՝ (−∞;−5)

ա) -6 բ) 1 գ) 5 դ) -1 ե) 20 զ) 10 է) -10 թ) -9

2. Պարզել՝ ճիշտ է, թե սխալ հետևյալ պնդումը՝ −12∈(−12;7]

ա) սխալ է  բ) ճիշտ է

3. Ո՞ր թվեր են պատկանում տրված հատվածին՝  [−12;0]

ա) −9  բ) −10 գ) 20  դ) −6  ե) −1 զ) 10  է)1   թ)5

4. Ո՞ր թվերը չեն պատկանում այս միջակայքին՝ (−1;10)

  ա) 12  բ) 1  գ) 10  դ) −1   ե) 5  զ) 2

5. Ընտրիր x∈(−∞;−1] միջակայքի պատկերը թվային առանցքի վրա, եթե a=−1

• 
• 
• 
• 

6.Գրառել նշանակումը՝

7. Կարդալ թվային բազմության անվանումը և այն պատկերել այն կոորդինատային ուղղի վրա՝

8․ Թվարկել թվային բազմությանը պատկանող բոլոր ամբողջ թվերը․

9․ Կոորդինատային առանցքի վրա նշել այն թվերը, որոնք՝

10․Անվանել թվային բազմությանը պատկանող չորս ամբողջ թվեր՝

11․Գրառել նկարում պատկերված բազմությունները՝

Թեմա՝ Թվային անհավասարությունների հատկությունները:

a>b և c>d կամ  a<b և c<d անհավասարությունները (միևնույն նշանի) կոչվում են միանուն:

a>b և c<d կամ  a<b և c>d անհավասարությունները (հակառակ նշանի) կոչվում են հականուն:

Օրինակ

6>−5 և 25>17 անհավասարությունները միանուն են, իսկ -41<−5 և 36>17 անհավասարությունները՝ հականուն:

Անհավասարությունների գումարումը

Եթե a>b և c>d, ապա a+c>b+d

Միանուն անհավասարությունները կարելի է գումարել :

Օրինակ՝ Ունենք երկու անհավասարություն՝ 5<10 և 4<9, գումարելով անհավասարության երկու մասերը, կստանաք՝ 5+4<10+9, 9<19։

Եթե a−ն,b−ն,c−ն,d−ն դրական թվեր են և a>b, c>d, ապա ac>bd

Եթե դրական ձախ և աջ մասերով միանուն անհավասարությունները բազմապատկենք, ապա կստացվի միանուն անհավասարություն (նշանը չի փոխվի):

Անհավասարության աստիճան բարձրացնելը

Եթե a և b թվերը դրական են a<b, ապա aⁿ<bⁿ, որտեղ n -ը բնական թիվ է:  
Եթե դրական ձախ և աջ մասերով միանուն անհավասարումները բարձրացնել միևնույն բնական աստիճանի, ապա կստացվի միանուն անհավասարություն (նշանը չի փոխվի):

Օրինակ՝  Քանի, որ 2<3, ապա քառակուսի բարձրացնելով, ստանում ենք ևս մեկ ճիշտ անհավասարություն՝  2²=4,  3²=9, 4<9

Առաջադրանքներ։

1․Գումարել թվային անհավասարությունները։

ա) 18>11 և 15>7,  բ) -4>-6 և 13>8  գ) -16<-7 և 12<37, դ) -9<0 և 5<19

Ա 18+15>11+7=33>18

Բ -4+13>-6+8=9>2

Գ -16+12<-7+37=-4<30

Դ -9+5<0+19=-4<19

2. Գումարել թվային անհավասարությունները։

Ա 14+10>11+9=24>20

Բ -2+3>-3+2=1>-1

Գ -6+2<-5+3=-4<-2

Դ -8+8<0+9=0<9

3․Բազմապատկել թվային արտահայտությունները։

ա) 14>10 և 2>1  բ) 5>3 և 6>5  գ) 6<7 և 2<3  դ) 8<9 և 1<2

Ա 14*2>10*1=28>10

Բ 5*6>3*6=30>18

Գ 6*2<7*3=12<21

Դ 8*1<9*2=8<18

4․Գումարել  անհավասարությունները: ա) 22>17 և 3.2>0.6 բ) 53<65 և 7,6<10,9

Ա 22+3,2>17+0,6=25,2>17,6

Բ 53+7,6<65+10,9=60,6<75,9

5․Զբոսաշրջիկ առաջին օրն անցավ 20 կմ-ից ավելի, իսկ երկրորդ օրը 25 կմ-ից ավելի։ Արդյո՞ք կարելի պնդել, որ զբոսաշրջիկն անցել է 45 կմ-ից ավելի ճանապարհ։ Պատասխանը հիմնավորել։

X=20

y=25

x+y=45

Պատ.՝ Այո

6․ Ուղղանկյան երկարությունը 13 սմ-ից փոքր է, իսկ լայնությունը՝ 5 սմ-ից փոքր։Արդյո՞ք կարելի պնդել, որ ուղղանկյան մակերեսը 65 սմ²-ից ավելի է։ Պատասխանը հիմնավորել։

13սմ*5սմ=65սմ Բայց քանի որ խնդրում տրված է, որ լայնությունը 5 սմ-ից փոքր է, իսկ երկարությունը 13 սմ-ից է փոքր ապա դա չի կարող լինել 13*5, պետք է լինի օրինակ 12*4=48, այդ պատճառով մենք չենք կարող պնդել, որ ուղղանկյան մակերեսը 65սմ-ից ավելի է:

Թեմա՝ Թվային անհավասարությունների հատկությունները:

Իրական թվերի կանոնները

Իրական թվերը ենթարկվում են հետևյալ կանոններին:

1 -ին կանոն: Ցանկացած երկու a և b իրարից տարբեր իրական թվերից մեկը մյուսից մեծ է: Այսինքն, ցանկացած a և b իրական թվերի համար տեղի ունի հետևյալ առնչություններից միայն մեկը՝ a=b, a>b, a<b

Օրինակ՝ 10 և 15 թվերի համար ճիշտ է 10<15 անհավասարությունը, և սխալ են մյուս երկու առնչությունները՝ 10=15 և 10>15 

2 -րդ կանոն: Ցանկացած երկու a և b իրարից տարբեր իրական թվերի միջև կա երրորդ թիվը: Այսինքն`  եթե a<b, ապա գոյություն ունի այնպիսի c թիվ, որ տեղի ունի հետևյալ երկկողմանի անհավասարությունը՝ a<c<b

Օրինակ՝ 1.4 և 1.5 թվերի համար գոյություն ունի, օրինակ, 1.44 թիվը, այնպես, որ տեղի ունի հետևյալ երկկողմանի անհավասարությունը՝ 1.4<1.44<1.5 

3 -րդ կանոն: Ցանկացած երեք a, b և c իրական թվերի համար, եթե a<b և b<c, ապա a<c

Օրինակ՝ 10/11<1 և 1<6/5 անհավասարություններից բխում է 10/11<6/5 անհավասարությունը:

Թվի գումարումը և թվով բազմապատկումը 

1 -ին հատկություն: Եթե a>b, ապա a+c>b+c

Եթե անհավասարության երկու մասերին գումարել կամ հանել միևնույն թիվը, ապա անհավասարության նշանը չի փոխվի:

Օրինակ՝ 3<12 ճիշտ անհավասարության երկու մասերին գումարելով −2 թիվը, կստանանք ճիշտ անհավասարություն՝  1<10

2 -րդ հատկություն: Եթե a>b և k>0, ապա ak>bk

Եթե անհավասարության երկու մասերը բազմապատկել միևնույն դրական թվով, ապա անհավասարության նշանը չի փոխվի:

Օրինակ Գիտենք, որ 17,2<x<17,3: Դրտարկենք 2x -ը:

Կրկնակի անհավասարությունը դրական 2 թվով բազմապատկելիս ստացվում է միանուն անհավասարություն (նշանները չեն փոխվում):

17,2⋅2<x⋅2<17,3⋅2,     34,4<2x<34,6

3 -րդ հատկություն: Եթե a>b և k<0, ապա ak<bk

Եթե անհավասարության երկու մասերը բազմապատկել միևնույն բացասական թվով, ապա անհավասարության նշանը կփոխվի:

Օրինակ՝ Հայտնի է, որ 17,2<x<17,3: Դիտարկենք −2x-ը:

Կրկնակի անհավասարությունը բացասական −2 թվով բազմապատկելիս ստացվում է հականուն անհավասարություն (նշանները փոխվում են):

17,2⋅(−2)<x⋅(−2)<17,3⋅(−2),   −34,4>−2x>−34,6,   −34,6<−2x<−34,4

Առաջադրանքներ

1.Համեմատել

Ա <

Բ >

Գ =

Դ <

Ե <

Զ <

2. Երկու ճշմարիտ անհավասարությունների հիման վրա կատարել եզրակացություն.

Ա <

Բ <

Գ >

Դ >

Ե >

Զ <

Է <

Ը <

3.Նշել տրված թվերից մեկից մեծ և մյուսից փոքր թիվ: Պատասխանը գրել կրկնակի անհավասարության տեսքով:

Ա 3<4<5

Բ -25>-27>-29

Գ 2,50<2,55<2,60

Դ 2,4<2,402<2,404

Ե 3,710>3,715>3,720

Զ -0,501<0,600<0,601

4.Գրել անհավասարություն, որը ստացվում է տված անհավասարության ձախ և աջ մասերի թվերը փոխարինելով նրանց հակադարձներով:

Ա 1/6<1/3

Բ 1/7>1/10

Գ 1/2>1/4

Դ 1/11>1/12

Ե 1/13<1/12

Զ 1/15>1/26

5. Տրված ճշմարիտ անհավասարությունից ստանալ ճշմարիտ անհավասարություն,որում յուրաքանչյուր թիվը փոխարինված է իր հակադիրով:

Ա -3<0

Բ -5<-1

Գ 9>1

Դ 5>1

Ե -9<-2

Զ 0>-3

6. Տրված ճշմարիտ անհավասարությունից ստանալ նոր ճշմարիտ անհավասարություն` գումարելով նրա երկու մասերին միևնույն թիվը.

 ա)14<21  բ) 32> 27  գ) 45<78  դ) -55<88   ե) -5 > -15  զ) 64> -99

Ա 14+7<21+7

Բ 32+15>27+15

Գ 45+45<78+45

Դ -55+88<88+88

Ե -5+15>-15+15

Զ 64+16>-99+16

7. Տրված ճշմարիտ անհավասարությունից ստանալ նոր ճշմարիտ անհավասարություն` նրա երկու մասը բազմապատկելով միևնույն դրական թվով.

Ա 15*5<20*5

Բ 5*10>4*10

Գ -2.5*3<3.3

Դ 1,1*4<1,2*4

Ե 1,3*7>1,2*7

Զ -5*5<6*5

8. Բազմապատկել ճշմարիտ անհավասարության երկու մասը միևնույն բացասական թվով:

Ա -1>-2

Բ -5<-4,5

Գ -6.5>-6.9

Դ -1.1>-1.2

Ե -1.3<-1.2

Զ -5>-6

9. Համեմատել

Ա <

Բ <

Գ <

Դ <

Ե <

Զ >

Է <

Ը =

Թ >

Ժ <

Ի <

Լ <

Թեմա՝ Իրական թվեր» թեմայի ամրապնդում։

Առաջադրանքներ։

1․ Պարզել a³b⁵c⁶d⁹ արտահայտության նշանը, եթե a>0,b<0,c<0,d>0

a³b⁵c⁶d⁹<0

2․ Գրել տրված թվի մոտավոր արժեքը պակասորդով՝ մինչև 0,01 ճշտությամբ՝

ա) 1.73121314151617≈1.73

բ) 3.84752136124584≈3.84

գ) 5.54210362151617≈5.54

3․ Տրված թվերը կլորացնելով 0,1 ճշտությամբ` գտնել նրանց մոտավոր գումարը.

ա) 3,288 + 0,123=3,3+0,1=3,4

բ) 0,100100010… + 0,238=0,1+0,2=0,3

գ) -1, 236 + 2, 555=-1,2+2,6=1.4

դ)2, 7(3) + 3 ,(42)=6.1

4․ Մինչև 0,01 ճշտությամբ կլորացնել թվերը և հաշվել նրանց մոտավոր գումարն ու տարբերությունը, եթե

ա) a=0,657 b=0,146= 0,76+0.15=0.91, 0,76-0,15=0,61 բ) a=5,4879  b=-0,250145= 5,59+(-0,35)=5.24, 5,59-(-0,35)=5.94

գ) a=-0,078 b=-0,682= -0,18+(-0,78)=-0.96, -0,18-(-0,78)=0.6     դ) a=5,(7)  b=6,(5)=5,77+6,55=12.32, 5,77-6,55=0,78

5. Նշել մի որևէ թիվ, որը գտնվում է տված թվերի միջև

ա) a=5,6 b=5,7     բ) a=4,5 b=4,(5)    գ) a=-2,27  b=-2.26

Ա.5,63

Բ 4,53

Գ -2,23

Թեմա՝ Թվաբանական գործողություններ իրական թվերի հետ։

a,b,c իրական թվերի համար տեղի ունեն գումարման և բազմապատկման ընդունված կանոնները՝

a+b=b+a    ab=ba     a+(b+c)=(a+b)+c   a(bc)=(ab)c    (a+b)c=ac+bc:

Տեղի ունեն նաև թվերի նշանների վերաբերյալ հետևյալ կանոնները՝ 

— երկու դրական թվերի արտադրյալը (քանորդը) դրական թիվ է,
— երկու բացասական թվերի արտադրյալը (քանորդը) դրական թիվ է,
— դրական և բացասական թվերի արտադրյալը (քանորդը) բացասական թիվ է: 

Թվաբանական գործողությունները իրական թվերի հետ ունեն հետևյալ հատկությունները:

1. Ռացիոնալ թվերի հետ ցանկացած թվաբանական գործողության (բացի 0-ի վրա բաժանելուց) արդյունքում ստացվում է ռացիոնալ թիվ:

2. Իռացիոնալ թվերի հետ թվաբանական գործողության արդյունքում կարող է ստացվել ինչպես ռացիոնալ, այնպես էլ իռացիոնալ թիվ:

3. Ռացիոնալ և իռացիոնալ թվերի հետ թվաբանական գործողության (բացի 0-ի վրա բաժանելուց և բազմապատկելուց) արդյունքում ստացվում է իռացիոնալ թիվ:

Բերված կանոններն ու հատկությունները տեսական բնույթ ունեն: Հիշում ենք, որ իրական թվերը անվերջ տասնորդական կոտորակներ են: Այդ պատճառով, գործնականում, հարմար է թվաբանական գործողությունները կատարել մոտավոր հաշված (կլորացրած) կոտորակների հետ:

Երկու իրական թվերի գումարը (տարբերությունը) մոտավոր հաշվելու համար նախ այդ թվերը կլորացնում են նույն ճշտությամբ, ապա գումարում են (հանում են) ստացված մոտավորությունները: 

Օրինակ

Մոտավոր հաշվենք a=3.889217010203… և b=−1.260076(27)… թվերի գումարը մեկ հարյուրերորդականի ճշտությամբ: 

1) Կլորացնենք այս թվերը մեկ հարյուրերորդականի ճշտությամբ՝

a≈3.89,b≈−1.26:

2) Կատարենք գումարումը՝

a+b≈3.89+(−1.26)==3.89−1.26=2.63:

Երկու իրական թվերի արտադրյալը (քանորդը) մոտավոր հաշվելու համար նախ այդ թվերը կլորացնում են նույն ճշտությամբ, բազմապատկում են (բաժանում են) ստացված մոտավորությունները, ապա արդյունքը կլորացնում են նույն ճշտությամբ:

Օրինակ

Մոտավոր հաշվենք վերևի c=4.579(128) և 2.1122334455… թվերի  արտադրյալը մեկ հարյուրերորդականի ճշտությամբ:

1) Կլորացնենք այս թվերը մեկ հարյուրերորդականի ճշտությամբ՝

c≈4.58,d≈2.11:

2) Կատարենք բազմապատկումը՝

c⋅d≈4.58⋅2.11=9.6638:

3) Կլորացնենք բազմապատկման արդյունքը նույն ճշտությամբ՝

c⋅d≈9.66:

Այսպիսով, առավել անկանխատեսելի է այն դեպքը, երբ գործողությունները կատարվում են երկու իռացիոնալ թվերի հետ: Այս դեպքում արդյունքը կարող է լինել ինչպես ռացիոնալ, այնպես էլ իռացիոնալ թիվ:

Օրինակ

ա) √3⋅√3=3  իռացիոնալ թվերի արտադրյալը տալիս է ռացիոնալ թիվ:

բ) √3⋅√5=√15  իռացիոնալ թվերի արտադրյալը տալիս է իռացիոնալ թիվ:

Հիշենք, որ ցանկացած իրական թիվ անվերջ տասնորդական կոտորակ է՝

— ռացիոնալ թվերն անվերջ պարբերական կոտորակներ են, իսկ

— իռացիոնալ թվերը՝ անվերջ ոչ պարբերական կոտորակներ:

Ուստի, գործնականում, հարմար է թվաբանական գործողությունները կատարել մոտավոր հաշված (կլորացրած) կոտորակների հետ:

1) Երկու իրական թվերի գումարը (տարբերությունը) մոտավոր հաշվելու համար նախ այդ թվերը պետք է կլորացնել նույն ճշտությամբ, ապա գումարել (հանել) ստացված արդյունքները:  

2) Երկու իրական թվերի արտադրյալը (քանորդը) մոտավոր հաշվելու համար նախ այդ թվերը պետք է կլորացնել նույն ճշտությամբ, բազմապատկել (բաժանել) ստացված մոտավորությունները, ապա արդյունքը կլորացնել նույն ճշտությամբ:

Առաջադրանքներ

1․Մինչև 0,1 ճշտությամբ կլորացնել թվերը և հաշվել նրանց մոտավոր գումարն ու տարբերությունը, եթե

ա) a= 3,28 b= 0,11  բ) a=-7,17 b= -0,33 գ) a=2,7235 b=-3,42426  դ) a=2,7(3) b=3,4(2)

Ա. 3,3+0,1=3,4, 3,3-0,1=3,2

Բ -7,2+(-0,3)=-7,5, -7,2-(-0,3)=-6,9

Գ a=2,7+(-3,4)=-0,7, 2,7-(-3,4)=6,1

Դ a=2,7+3,4=6,1, 2,7-3,4=-0,7

2․Մինչև 0,01 ճշտությամբ կլորացնել թվերը և հաշվել նրանց մոտավոր գումարն ու տարբերությունը, եթե

ա) a=1,4545 b=-1,203      բ) a=2,1264  b=-3,1145 

գ) a=-5,777 b= 2,536      դ) a=0,5642  b=-3,573 

Ա 1,45+(-1,20)= 0,25, 1,45-(-1,20)=2,65

Բ 2,13+(-3,11)=-0,98, 2,13-(-3,11)=5,24

Գ 5,78+2,54=8,32, 5,78-2,54=3,24

Դ 0,56+(-3,57)=-3.01, 0,56-(-3,57)=4,13             

3․Մինչև 0,1 ճշտությամբ կլորացնել թվերը և հաշվել նրանց մոտավոր արտադրյալն ու քանորդը, եթե

ա) a=-2,435 b=1,923       բ) a=2,14564  b=0,78788 

գ) a=-5,768 b= 2,534      դ) a=0,56  b=0,(3)

Ա -2,4*1,9=-4.56, -2,4:1,9=-1.26

Բ 2,1*0,8=1.68, 2,1:0,8=2.625

Գ -5,8*2,5=-14.25, -5,8:2,5=-2.32

Դ 0,6*0,3=0,18, 0,6:0,3=2

4․Մինչև 0,01 ճշտությամբ կլորացնել թվերը և հաշվել նրանց մոտավոր գումարն ու տարբերությունը, եթե

ա) a=0,253 b=0,75        բ) a=3,5781  b=-0,08788 

գ) a=-0,045 b= -0,593      դ) a=4,(2)  b=1,(3)   ե ) a=0,(2) b=2

Ա=0,25+0,75=1, 0,25-0,75=-0,50

Բ 3,58+(-0,09)=3,49, 3,58-(0,09)=3,67

Գ -0,04+(-0,59)=-0,63, -0,04-(-0,59)=0,55

Դ 4,22+1,33=5,55, 4,22-1,33=2,89

Ե 0,22+2,00=2,22, 0,22-2,00=-1.88

5.Նշել մի որևէ թիվ, որը գտնվում է տված թվերի միջև

ա) a=2,3 b=2,4     բ) a=3,2 b=3,(2)    գ) a=-3,15 b=-3,14

Ա 2,31

Բ 3,21

Գ -3,148

6․ Ճի՞շտ է արդյոք անհավասարությունը․

ա)  3,5+2,729<3,6+2,729    բ)  -3,21+0,(4)<-3+0,(4)    գ) -5,6+3,2>-5,1+3,(2)

դ) 3,7⋅0,8< 3,8⋅0,8       ե) -5,1⋅0,(3)< -5⋅0,(3)     զ) -3,(8)⋅0,5>-3,8⋅0,(5)

Ա Ճիշտ է

Բ Ճիշտ է

Գ Սխալ է

Դ Ճիշտ է

Ե Ճիշտ է

Զ Սխալ է

Թեմա՝ Իրական թվերի համեմատումը և մոտարկումը։

Եթե ունենք երկու իրական թիվ, ապա՝ կամ դրանք իրար հավասար են, կամ էլ՝ մեկը մյուսից մեծ է: Պարզենք, թե գործնականում ինչպե՞ս համեմատել իրական թվերը:

Երկու անվերջ տասնորդական կոտորակներ (այսինքն իրական թվեր) իրար հավասար են, եթե նրանք ունեն նույն նշանը և նրանց մոդուլներն ունեն նույն ամբողջ մասերը և համապատասխան կարգերում նույն թվանշանները:

Զրո թիվը փոքր է ցանկացած դրական թվից և մեծ է ցանկացած բացասական թվից:

Նկարագրենք իրարից տարբեր երկու տասնորդական կոտորակների (այսինքն իրական թվերի) համեմատման քայլերը:

Առաջին քայլ: Եթե երկու դրական տասնորդական կոտորակների ամբողջ մասերը իրարից տարբեր են, ապա մեծ է այն կոտորակը, որի ամբողջ մասն ավելի մեծ է:

Եթե ամբողջ մասերը հավասար են, կատարում ենք երկրորդ քայլը:

Երկրորդ քայլ: Դիտարկում ենք ստորակետից հետո եկող առաջին կարգը: Այն կոտորակն է ավելի մեծ, որի այդ կարգում գրված թվանշանը ավելի մեծ է:

Եթե առաջին կարգում գրված թվանշաններն էլ են իրար հավասար, ապա կատարում ենք հաջորդ քայլը և դիտարկում ենք ստորակետից հետո եկող երկրորդ կարգը և այդպես շարունակ:

Վերջին քայլ: Քանի որ դիտարկում ենք իրարից տարբեր կոտորակներ, ապա հաջորդաբար դիտարկելով կոտորակների կարգերը, կհանդիպենք այնպիսի կարգի, որում գրված թվանշաններն իրար հավասար չեն: Այն կոտորակն է ավելի մեծ, որի այդ կարգում գրված թվանշանը ավելի մեծ է:

Օրինակ

Համեմատենք 2.1 և 2.(1) իրական թվերը:

Կոտորակները գրենք անվերջ տասնորդական կոտորակների տեսքով և կիրառենք համեմատման նկարագրված քայլերը՝ 2.1=2.1000…2.(1)=2.1111…

Առաջին քայլ: Նկատում ենք, որ կոտորակների ամբողջ մասերը հավասար են իրար և հավասար են 2 -ի:

Երկրորդ քայլ: Իրար հավասար են նաև ստորակետից հետո եկող առաջին կարգային թվանշանները: Դրանք հավասար են 1 -ի:

Երրորդ քայլ: Առաջին կոտորակի երկրորդ կարգային թվանշանը 0 -ն է, իսկ երկրորդ կոտորակինը՝ 1 -ը:

Այսպիսով՝ 2.1<2.(1)

Որոշ դեպքերում, մասնավորապես, գրաֆիկական եղանակով հավասարումներ լուծելու համար, մաթեմատիկոսները որոշեցին մտցնել արժեքի մոտավոր հաշվման գաղափարը:

Մոտավոր հաշվարկի համար կա ևս մեկ պատճառ՝ դա իրական թվերն են, այսինքն՝ անվերջ տասնորդական կոտորակները: Չէ՞ որ կատարել հաշվարկներ անվերջ տասնորդական կոտորակների հետ անհարմար է, այդ պատճառով, գործնականում հաշվարկները կատարում են իրական թվերի մոտավոր արժեքների հետ:  

Երկրաչափական շատ բանաձևերում հանդիպում է π իրական թիվը: Դա անվերջ ոչ պարբերական տասնորդական կոտորակ է:

Օրինակ

Հաշվենք π=3,141592… թվի մոտավոր արժեքները:

1) Եթե այս անվերջ կոտորակի գրառումն ընդհատենք, ստորակետից հետո պահելով երկու թվանշան, ապա կստանանք՝ π≈3,14:

Սա π թվի մոտարկումն է հարյուրերորդականի ճշտությամբ (մինչև 0,01 ճշտությամբ) պակասորդով (ներքևից):

2) Ստորակետից հետո կարելի է պահել երեք թվանշան: Ստանում ենք՝ π≈3,141:

Սա π թվի մոտարկումն է մինչև 0,01 ճշտությամբ պակասորդով (ներքևից):

3) Եթե պահել երեք թվանշան և երրորդը մեկով ավելացնել՝ π≈3,142, ապա կստանանք π թվի մոտարկումը մինչև 0,01 ճշտությամբ ավելուրդով (վերևից):

Պակասորդով և հավելուրդով մոտարկումները անվանում են թվի կլորացում:

Կլորացման ճշտությունը որոշվում է թվի x ճշգրիտ արժեքի և նրա a մոտավոր արժեքի տարբերության մոդուլով՝ |x−a|

Կլորացման կանոնը:

Եթե առաջին դեն նետվող թիվը 5-ից փոքր է, ապա այն կարելի է ուղղակի անտեսել՝ կատարել մոտարկում պակասորդով, իսկ եթե դեն նետվող թիվը 5-ց մեծ է կամ հավասար, ապա պետք է կլորացնել հավելուրդով:

Ուշադրություն

Պետք է հիշել, որ պակասորդով կլորացնելիս միշտ ստանում ենք ճշգրիտից փոքր թիվ, իսկ հավելուրդով` մեծ:

Վերադարնանք π=3,141592… թվին: Կլորացնելով 0,001 ճշտությամբ ստանում ենք՝ π≈3,142: Այստեղ առաջին դեն նետվող թիվը հավասար է 5 -ի (ստորակերից հետո չորրորդ թիվը), ուստի կլորացրեցինք հավելուրդով: 

Օրինակ

Կլորացնելով 0,0001 ճշտությամբ ստանում ենք՝ π≈3,1416: Առաջին դեն նետվող թիվը (հինգերորդը ստորակետից հետո) հավասար է 9 -ի:

Արդեն տեսանք, որ 0,01 ճշտությամբ պետք է կլորացնել պակասորդով՝ π≈3,14:

Հարցեր և առաջադրանքներ։

1․ Ինչպե՞ս է կատարվում իրական թվերի համեմատումը։

Առաջին քայլ: Եթե երկու դրական տասնորդական կոտորակների ամբողջ մասերը իրարից տարբեր են, ապա մեծ է այն կոտորակը, որի ամբողջ մասն ավելի մեծ է:

Եթե ամբողջ մասերը հավասար են, կատարում ենք երկրորդ քայլը:

Երկրորդ քայլ: Դիտարկում ենք ստորակետից հետո եկող առաջին կարգը: Այն կոտորակն է ավելի մեծ, որի այդ կարգում գրված թվանշանը ավելի մեծ է:

Եթե առաջին կարգում գրված թվանշաններն էլ են իրար հավասար, ապա կատարում ենք հաջորդ քայլը և դիտարկում ենք ստորակետից հետո եկող երկրորդ կարգը և այդպես շարունակ:

Վերջին քայլ: Քանի որ դիտարկում ենք իրարից տարբեր կոտորակներ, ապա հաջորդաբար դիտարկելով կոտորակների կարգերը, կհանդիպենք այնպիսի կարգի, որում գրված թվանշաններն իրար հավասար չեն: Այն կոտորակն է ավելի մեծ, որի այդ կարգում գրված թվանշանը ավելի մեծ է:

2․ Ինչպե՞ս են կլորացնում իրական թվերը։

Եթե առաջին դեն նետվող թիվը 5-ից փոքր է, ապա այն կարելի է ուղղակի անտեսել՝ կատարել մոտարկում պակասորդով, իսկ եթե դեն նետվող թիվը 5-ց մեծ է կամ հավասար, ապա պետք է կլորացնել հավելուրդով:

Ուշադրություն

Պետք է հիշել, որ պակասորդով կլորացնելիս միշտ ստանում ենք ճշգրիտից փոքր թիվ, իսկ հավելուրդով` մեծ:

Վերադարնանք π=3,141592… թվին: Կլորացնելով 0,001 ճշտությամբ ստանում ենք՝ π≈3,142: Այստեղ առաջին դեն նետվող թիվը հավասար է 5 -ի (ստորակերից հետո չորրորդ թիվը), ուստի կլորացրեցինք հավելուրդով: 

Օրինակ

Կլորացնելով 0,0001 ճշտությամբ ստանում ենք՝ π≈3,1416: Առաջին դեն նետվող թիվը (հինգերորդը ստորակետից հետո) հավասար է 9 -ի:

Արդեն տեսանք, որ 0,01 ճշտությամբ պետք է կլորացնել պակասորդով՝ π≈3,14:

3․ Համեմատել թվերը.

Ա >

Բ >

Գ <

Դ <

Ե =

Զ =

4.Թվերը դասավորել աճման կարգով․

Ա -2,(7) -0,142536, 0,125, 0,1(25)

Բ -2(778), 0,(12), 1,(5)

5․Թվերը դասավորել նվազման կարգով․

1/8, 0,124, 0,1115, 1/9, -4,7(5), -4,7556

6․ Գտե՛ք a թվի մոտարկումը պակասորդով՝ ստորակետից հետո երկրորդ կարգի 1 միավորի ճշգրտությամբ, եթե․

ա) a=0,76543   բ) a=-0,34354

Ա. a=0,8

Բ. -0,3

7․ Գտե՛ք a թվի մոտարկումը հավելուրդով՝ ստորկետից հետո երկրորդ կարգի 1 միավոր ճշգրտությամբ, եթե
ա) a=3,56789  բ) a=2,555 ․

Ա a=3,57

Բ a=2,55

8․ a թիվը կլորացրեք 0,001 ճշգրտությամբ, եթե․
ա) a=8,91011…
բ) a=-8,910111…
գ) a=0,2626
դ) a=0,6265

Ա) 8,910

Բ) -8,910

Գ) 0,263

Դ) 0,626

Առաջին ուսումնական շրջանի ամփոփում։

1.

Ա (x+y)/6

Բ (a-b)/3

Գ x/9

Դ (8a+3b)/24

Ե 7x/9a²

Զ 2m/3

Է x/4(x-y)

2.

Ա 3

Բ -5

Գ 0

3.

Ա 0

Բ -3

Գ 5

4.

Ա 4

Բ 0

Գ 5

5.

Ա 3/5

Բ 16/5

Գ 2/9

Թեմա՝ Պարբերական և անվերջ ոչ պարբերական կոտորակներ:

m/n տեսքի թվերը, որտեղ m-ը ամբողջ թիվ է, իսկ n-ը բնական թիվ, կոչվում են ռացիոնալ թվեր: Ռացիոնալ թվերի բազմությունը նշանակում են Q տառով:

7/22-րդ սովորական կոտորակի դեպքում օգտվենք «անկյունով» բաժանման եղանակին:

Երևում է, որ, սկսած երկրորդ թվանշանից, ստորակետից հետո կրկնվում է թվերի մի խումբ՝ մեկն ու ութը՝ 18,18,18,…: Այսպիսով, 7/22=0,3181818…: Կարճ դա գրում են այսպես՝ 0,3(18):Այսպիսով, մեզ հաջողվեց 7/22 -րդ սովորական կոտորակը ներկայացնել անվերջ պարբերական տասնորդական կոտորակի տեսքով:Փորձենք ռացիոնալ թվերը ներկայացնել տասնորդական կոտորակների տեսքով:Պարզվում է, որ ցանկացած ռացիոնալ թիվ կարելի է գրել անվերջ տասնորդական կոտորակի տեսքով:

ա) 7 ամբողջ թիվը կարելի է գրել 7,0000… անվերջ տասնորդական կոտորակի տեսքով:

բ) 4,244 վերջավոր տասնորդական կոտորակը կարելի է գրել 4,244000… անվերջ տասնորդական կոտորակի տեսքով:

գ) 5/11 սովորական կոտորակը անվերջ տասնորդական կոտորակի տեսքով գրելու համար օգտվենք «անկյունով» բաժանման եղանակից:

Տեսնում ենք, որ թվերի մի խումբ կրկնվում է՝ 45,45,45:Այսպիսով՝ 5/11 =0,454545…: Կարճ գրում ենք այսպես՝ 0,(45)

Ստորակետից հետո թվանշանների կրկնվող խումբը կոչվում է պարբերություն, իսկ ինքը կոտորակը՝ անվերջ պարբերական տասնորդական կոտորակ:  

Բերված օրինակներում 7 բնական թիվը, 4,244 վերջավոր տասնորդական կոտորակը և 5/11 սովորական կոտորակը ներկայացրեցինք անվերջ պարբերական կոտորակների տեսքով՝

ա) 7=7,00000…=7,(0)

բ) 4,244=4,244000…=4,244(0)

գ) 511 =0,454545…=0,(45)

Ցանկացած ամբողջ թիվ և ցանկացած վերջավոր տասնորդական կոտորակ կարելի է համարել 0 պարբերությամբ պարբերական տասնորդական կոտորակ:Ցանկացած ռացիոնալ թիվ կարելի է ներկայացնել անվերջ պարբերական տասնորդական կոտորակի տեսքով:

Եթե m/n անկրճատելի կոտորակի հայտարարը 2-ից և 5-ից տարբեր պարզ արտադրիչ ունի, ապա այդ կոտորակը չի վերածվում վերջավոր տասնորդական կոտորակի։

Կան անվերջ տասնորդական կոտորակներ, որոնք պարբերական չեն:

Օրինակ

0,10110111… (յուրաքանչյուր 0-ից հետո 1-երի թիվը մեկով ավելանում է),

−17,1234567891011121314… (ստորակետից հետո գրված են բոլոր բնական թվերը):

Կան նաև երկրաչափությունից հայտնի անվերջ ոչ պարբերական տասնորդական կոտորակներ:

Եթե ցանկացած շրջանագծի երկարությունը բաժանել նրա տրամագծի վրա, ապա քանորդում ստացվում է իռացիոնալ թիվ: Այդ թիվը հանրահայտ π=3,1415926535897932… թիվն է (π-ն հունարեն այբուբենի տառ է, կարդացվում է «պի»):

π թվի իռացիոնալությունը ապացուցվել է գերմանացի մաթեմատիկոս Ի.Լամբերտի կողմից 1766 թվականին:  

Թիվը, որը կարելի է գրել անվերջ ոչ պարբերական կոտորակի տեսքով, կոչվում է իռացիոնալ թիվ:

Ռացիոնալ և իռացիոնալ թվերը միասին անվանում են իրական թվեր: Իրական թվերի բազմությունը նշանակում են R տառով:

Այսպիսով, կան երկու տեսակի իրական թվեր՝

• ռացիոնալ թվեր,
• իռացիոնալ թվեր:

Թվերը ներկայացնելով տասնորդական կոտորակների տեսքով, գալիս ենք հետևյալ եզրակացությանը: Իրական թվերը բաղկացած են տասնորդական կոտորակներից՝

• վերջավոր և անվերջ պարբերական տասնորդական կոտորակներից (ռացիոնալ թվեր),
• անվերջ ոչ պարբերական տասնորդական կոտորակներից (իռացիոնալ թվեր):

Հարցեր և առաջադրանքներ։

1․Ո՞ ր թվերն են կոչվում ռացիոնալ թվեր: m/n տեսքի թվերը, որտեղ m-ը ամբողջ թիվ է, իսկ n-ը բնական թիվ, կոչվում են ռացիոնալ թվեր:                        2․Ի՞նչն է կոչվում պարբերություն։ Ստորակետից հետո թվանշանների կրկնվող խումբը կոչվում է պարբերություն, իսկ ինքը կոտորակը՝ անվերջ պարբերական տասնորդական կոտորակ:                                 

3․Ո՞ր թիվն է կոչվում իռացիոնալ թիվ։ Թիվը, որը կարելի է գրել անվերջ ոչ պարբերական կոտորակի տեսքով, կոչվում է իռացիոնալ թիվ:                             

4․Ո՞ր թվերն են կոչվում իրական թվեր։ Ռացիոնալ և իռացիոնալ թվերը միասին անվանում են իրական թվեր:

5․Տրված թիվը գրառել պարբերական կոտորակի տեսքով, նշել պարբերությունը․

Ա 0,(33)

Բ 0,(22)

Գ 2,4

Դ 12,000000

Ե 0,8

Զ 0,75

Է 0,57

Ը 0,714

Թ 0,1(66)

Ժ 0,(33)

Ի 0,5

Լ 0,(66)

Խ 0,487

Ծ 0,(405)

Կ 0,2380

6․ Սովորական կոտորակը վերածել պարբերականի․                      

ա) 5/9=0,(55)

բ) 2/9=0,(22) 

գ) 4/9=0,(44)

դ) 6/9,=0,(66)

 ե) 7/9, = 0,(77)

 զ) 8/9= 0,(88)

է) 12/99=0,(12)

 ը) 23/99 0,(23)

 թ 34/99 0,(34)

 ժ) 89/99 =0,(89)

7. Օգտվելով նախորդ առաջադրանքներից՝ պարբերական կոտորակը գրառել սոեվորական կոտորակի տեսքով․ ա) 0,(1)=1/10  բ) 0,(3)=3/10  գ) 0,(5)=5/10=1/2  դ) 0,(25)=25/100=1/4  ե) 0,(37)=37/100  զ) 0,(89)=89/100

8. Նշեք չորս թիվ, որոնք լինեն

Ա. 1,2,3,4

Բ. 5,18,45,61

Գ. -2,-1, -9,-7

Դ. 100, 200,300,400

Ե. 1/2, 200/1000, 15/30, 33/66

Զ. 4/23, 2/6, 5/9, 8/17,

Է. 4,6,8,10

Ը. 3,5,7,9

Թ. 41,5,7,19

Ժ.4, 8,64,72

Ի. 6,12,9,15

Լ. 10,20,30,40

9. Նշեք երկու թիվ, որոնք լինեն

Ա. -1/4, -3/6

Բ 10,15

Գ 3,5

Դ 31,81

Ե 6,58

Զ 21,35

10. Ռացիոնա՞լ, թե՞ իռացիոնալ է հետևյալ թիվը․                        ա) 0,275  բ) 0,(2)  գ) 1,32323232․․․  դ) 3,10110111011110․․․․․  ե) 0,1234567891011․․

Ա Ռացիոնալ է

Բ պարբերական իռացիոնալ է

Գ պարբերական Իռացիոնալ է

Դ Իռացիոնալ է

Ե Իռացիոնալ է

Թեմա՝ Ռացիոնալ արտահայտություն և նրա թվային արժեքը։ Վարժությունների լուծում։

1. Արտահայտությունը գրել առանց բացասական աստիճանների.

Ա 1/a+1/b

Բ 1/(a+b)²

Գ a²b²/(b²-a²)

Դ a/a²+1

2. Հաշվել.

Ա) 3/10

Բ) 4/9

Գ) 8

3. Տառերի ինչպիսի՞ արժեքների դեպքում է որոշված արտահայտությունը

Ա 0

Բ 1

Գ -3

Դ 3

4.  Գտնել արտահայտության արժեքը.

Ա 0,96

Բ ?

Գ -4

Դ 31/3

5. Գտնել արտահայտության արժեքը.

Ա) 1/10

Բ) 2

Թեմա՝ Ռացիոնալ արտահայտություններ և դրանց թվային արժեքը:

Ռացիոնալ արտահայտություն կոչվում է այն արտահայտությունը, որում մի քանի հանրահաշվական կոտորակներ միացված են թվաբանական գործողությունների նշաններով:

Ընդ որում այդ արտահայտությունը չպետք է պարունակի զրոյական բազմանդամի վրա բաժանման գործողություն:

Հանրահաշվական կոտորակը նույնպես անվանում են ռացիոնալ արտահայտություն:

Օրինակ․

Ռացիոնալ են հետևյալ արտահայտությունները՝

Որպեսզի այսպիսի արտահայտությունները ճիշտ պարզեցնել, պետք է՝

•  պահպանել գործողությունների հերթականությունը,
•  պահպանել այդ գործողությունների կատարման կանոնները,
•  հիշել, որ բոլոր գործողությունները կատարվում են միայն այն արժեքների համար, որոնց դեպքում կոտորակներն իմաստ ունեն:

Օրինակ՝

Հարցեր և առաջադրանքներ:

1․ Ո՞ր արտահայտությունն է կոչվում ռացիոնալ:

Ռացիոնալ արտահայտություն կոչվում է այն արտահայտությունը, որում մի քանի հանրահաշվական կոտորակներ միացված են թվաբանական գործողությունների նշաններով:

2. Պարզեցնել ռացիոնալ արտահայտությունը.

Ա) bc+ac+ab

Բ) 5-5x+15x²

3. Արտահայտություններից որո՞նք իմաստ չունեն.

Ա) Իմաստ ունի

Բ) Իմաստ ունի

Գ) Իմաստ չունի որովհետև հայտարարը հավասար է 0-ի:

4. x-ի ինչպիսի թվային արժեքի համար հանրահաշվական կոտորակի արժեքը հավասար է 0-ի.

Ա. x=2

Բ. x=-4

Գ. x=2

Դ. x=-5/2

Ե. x=-1-ի դեպքում հայտարարը դառնում է զրո հետևաբար կոտորակի արժեքը զրո չի կարող լինել:

5. Գտնել արտահայտության արժեքը, երբ x=2

Ա) 2

Բ) 5

Գ) -2/7

Դ) 0

6. Հաշվել արտահայտության արժեքը.

Ա) 10/3

Բ) 235/25

Գ) 5/-3