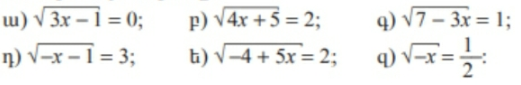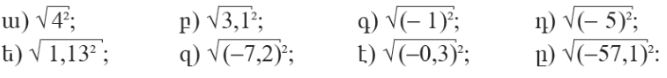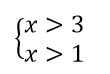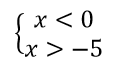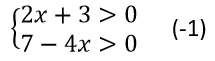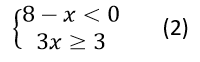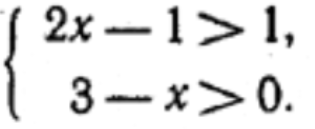Category: Հանրահաշիվ

Թեմա՝ Պարզագույն իռացիոնալ անհավասարումներ։

Եթե անհավասարման անհայտը գտնվում է քառակուսի արմատի նշանի տակ, ապա  այդպիսի անհավասարումը անվանում են իռացիոնալ: 

Սովորենք լուծել պարզագույն իռացիոնալ հավասարումները: Պարզագույն իռացիոնալ անհավասարումներն են՝ √x<a և √x>a, որտեղ a -ն տրված իրական թիվ է:

Դիտարկենք √x<a անհավասարումը:

1) Եթե a≤0, ապա թվաբանական քառակուսի արմատի սահմանման համաձայն, անհավասարումը լուծում չունի:

2) Եթե a>0, ապա պետք է անհավասարումը բարձրացնել քառակուսի և պահանջել, որ արմատն իմաստ ունենա (արմատատակ թիվը լինի ոչ բացասական): Եկանք հետևյալ համակարգին՝

Որպես պատասխան ստանում ենք հետևյալ կրկնակի անհավասարումը՝ 0≤x<a²

Դիտարկենք √x>a անհավասարումը:

1) Եթե a<0, ապա ձախից ոչ բացասական թիվ է, իսկ աջից՝ բացասական: Անհավասարումը միշտ ճիշտ է, եթե արմատն իմաստ ունի:

Հետևաբար այս դեպքում անհավասարման պատասխանը ԹԱԲ -ն է՝ [0;+∞)

2) Եթե a≥0, ապա պետք է անհավասարումը բարձրացնել քառակուսի և պահանջել, որ արմատն իմաստ ունենա (արմատատակ թիվը լինի ոչ բացասական): Գալիս ենք հետևյալ համակարգին՝

Որպես պատասխան ստանում ենք հետևյալ անհավասարումը՝ x>a²

Նման ձևով վարվելով՝ կարելի է լուծել պարզագույն ոչ խիստ անհավասարումները:

√x ≤a անհավասարման դեպքում գալիս ենք հետևյալ եզրակացություններին:

1) Եթե a<0, լուծում չկա: 

2) Եթե a≥0, ապա x∈[0;a2]

√x ≥ a անհավասարման դեպքում գալիս ենք հետևյալ եզրակացություններին:

1) Եթե a<0, պատասխանը ԹԱԲ -ն է՝ [0;+∞)

2) Եթե a≥0, ապա x∈[a2;+∞)

Օրինակ

Լուծենք √2x−1<3 իռացիոնալ անհավասարումը:

1) Սկզբում գտնենք ԹԱԲ -ը՝ 2x−1≥0

2) Երկու մասերը բարձրացնենք քառակուսի՝ (√2x−1)² ≥ 3²

3) Եկանք հետևյալ համակարգին՝

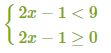
4) Լուծենք ստացված համակարգը՝

5) Պատասխանը ստացված բազմությունների հատումն է՝ x∈[0.5;5)

Առաջադրանքներ։

1․Լուծել անհավասարումները;

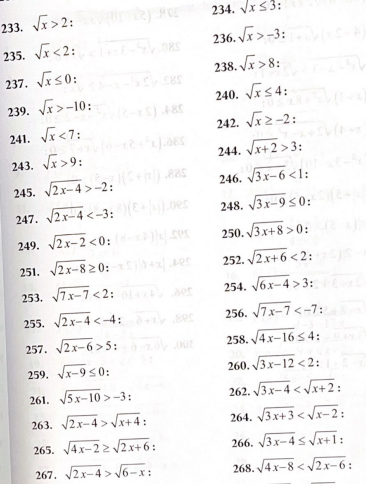
233. x∈(4,+∞)
234. x∈(0, 9)
235. x∈(0, 4)
236. x∈(0,+∞)
237. x=0
238. x∈(64,+∞)
239. x∈(0,+∞)
240. x∈(0, 16)
241. x∈(0, 49)
242. x∈(0,+∞)
243. x∈(81,+∞)
244. x∈(7,+∞)
245. x∈(2,+∞)
246. x∈(2, 7/3)
247. ∅
248. x=3
249. ∅
250. x∈(- 8/3,+∞)
251. x∈(4,+∞)
252. x∈(-3, -1)
253. x∈(1, 11/7)
254. x∈(13/6,+∞)
255. ∅
256. ∅
257. x∈(31/2,+∞)
258. x∈(4, 8)
259. x=9
260. x∈(4, 16/3)
261. x∈(2,+∞)
262. x∈(4/3, 3)
263. x∈(8,+∞)
264. ∅
265. x∈(4,+∞)
266. x∈(4/3, 5/2)
267. x∈(10/3, 6)
268. ∅

2․ Լուծել անհավասարումները։

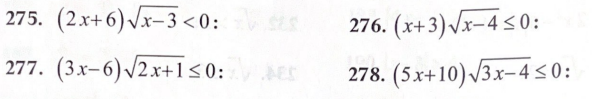
Ա լուծում չունի

Բ լուծում չունի

Գ լուծում չունի

Դ լուծում չունի

Թեմա` Պարզագույն իռացիոնալ հավասարումների լուժումը:

Եթե հավասարման անհայտը գտնվում է քառակուսի արմատի նշանի տակ, ապա այդպիսի հավասարումը անվանում են իռացիոնալ: 

Կյանքի շատ իրավիճակներ նկարագրվում են իռացիոնալ հավասարումներով: Ուստի, սովորենք լուծել գոնե պարզագույն իռացիոնալ հավասարումները:

Դիտարկենք 

Եթե հավասարման անհայտը գտնվում է քառակուսի արմատի նշանի տակ, ապա այդպիսի հավասարումը անվանում են իռացիոնալ: 

Կյանքի շատ իրավիճակներ նկարագրվում են իռացիոնալ հավասարումներով: Ուստի, սովորենք լուծել գոնե պարզագույն իռացիոնալ հավասարումները:

Դիտարկենք √2x+1=3 իռացիոնալ հավասարումը:

Ըստ քառակուսի արմատի սահմանման, այն նշանակում է, որ 2x+1=3²: Փաստորեն, քառակուսի բարձրացնելով, տրված իռացիոնալ հավասարումը բերեցինք 2x+1=9 գծային հավասարմանը:

Ուշադրություն

Քառակուսի բարձրացնելը իռացիոնալ հավասարումների լուծման հիմնական եղանակն է:

Դա բնական է, եթե պետք է ազատվել քառակուսի արմատի նշանից:

2x+1=9 հավասարումից ստանում ենք՝ x=4: Սա միաժամանակ  2х+1=9 գծային  և √2x+1=3  իռացիոնալ հավասարումների արմատն է:

Քառակուսի բարձրացնելու եղանակը տեխնիկապես բարդ չէ իրականացնել, սակայն երբեմն այն բերում է անցանկալի իրավիճակների:

Օրինակ

Դիտարկենք √2x−5=√4x−7 իռացիոնալ հավասարումը:

Երկու մասերը բարձրացնելով քառակուսի, ստանում ենք՝ (√2x−5)²=(√4x−7)² 2x−5=4x−7

Լուծելով ստացված 2x−4x=−7+5 հավասարումը, ստանում ենք x=1

Սակայն x=1, որը 2x−5=4x−7 գծային հավասարման արմատն է, չի բավարարում տրված իռացիոնալ հավասարմանը: Ինչո՞ւ: Իռացիոնալ հավասարման մեջ  փոխարեն տեղադրենք 1: Կստանանք՝ √−3=√−3

Հավասարումը բնականաբար չի բավարարվում, քանի որ հավասարության ձախ և աջ մասերը իմաստ չունեն։

Ստացել ենք ավելորդ արմատ: Այսպիսի իրավիճակներում ասում ենք, որ x=1 -ը թույլատրելի արժեք չէ, կամ չի պատկանում թույլատրելի արժեքների բազմությանը: Դուրս եկավ, որ այս դեպքում, իռացիոնալ հավասարումը արմատ չունի, մինչդեռ քառակուսի բարձրացնելուց ստացված գծային հավասարումը արմատ ուներ:

Պետք է այսպիսի ավելորդ արմատները ժամանակին հայտնաբերել և չընդգրկել լուծումների մեջ՝ դեն նետել: Դա արվում է ստուգման միջոցով: 

Իռացիոնալ հավասարումների համար, ստուգումը լուծման անհրաժեշտ փուլ է, որը օգնում է հայտնաբերել և դեն նետել ավելորդ արմատնելը: 

Ուշադրություն

Այսպիսով, իռացիոնալ հավասարումը լուծելու համար պետք է՝

1) այն բարձրացնել քառակուսի,

2) լուծել ստացված հավասարումը,

3) կատարել ստուգում՝ դեն նետելով ավելորդ արմատները,

4) գրել վերջնական պատասխանը:

Կիրառելով այս եզրակացությունը, դիտարկենք հետևյալ օրինակը:

Օրինակ

Լուծենք √5x−16=2 հավասարումը:

1) Երկու մասերը բարձրացնենք քառակուսի՝ (√5x−16)²=2²

2) Լուծենք ստացված հավասարումը՝

5x−16=4 5x=20 x=4

3) Կատարենք ստուգում: √5x−16=2 հավասարման մեջ տեղադրենք x=4: Ստանում ենք՝ √4=2 ճիշտ հավասարությունը:

4) Պատասխան՝ √5x−16=2 հավասարման լուծումը x=4 -ն է:

Հարցեր և առաջադրանքներ։

1․Ո՞ր հավասարումներն են կոչվում իռացիոնալ։

Եթե հավասարման անհայտը գտնվում է քառակուսի արմատի նշանի տակ, ապա այդպիսի հավասարումը անվանում են իռացիոնալ: 

2․ Ինչպե՞ս են լուծում պարզագույն իռացիոնալ հավասարումները։

1) այն բարձրացնել քառակուսի,

2) լուծել ստացված հավասարումը,

3) կատարել ստուգում՝ դեն նետելով ավելորդ արմատները,

4) գրել վերջնական պատասխանը:

3․ Լուծել հավասարումները։

Ա x=9

Բ x=0

Գ լուծում չունի

Դ 0,5

Ե 0,5

զ) -1

է) 44/3

ը) 48/5

թ) 7

4․ Լուծել հավասարումները։

ա) x=1/3a^2+1/3
բ) լուծում չունի
գ) x=2
դ) լուծում չունի
ե) x=8/5
զ) լուծում չունի

5․ Լուծել հավասարումները․

249.x=4
250.x=9
251.x=25
252.∅
253.x=0
254.x=81
255.x=64
256.∅
257.x=25
258.x=0
259.∅
260.x=25
261.x=6
262.x=20
263.x=6
264.x=6
265.∅
266.x=9
267.x=4,5
268.x=10
269.x=1
270.∅
271.x=3,3
272.x=1,3
273.x=6
274.∅
275.∅
276.x=7
277.∅
278.x=10
279.∅
280.x=0,75

1․ Պարզեցնել արտահայտությունը․

Ա 5√2

Բ √2

Գ -4√a

Դ (a-3)√x

Ե √a

Զ –√2

2․ Համեմատել արտահայտությունների արժեքները առանց արմատը հաշվելու։

Ա >

Բ >

Գ <

Դ <

Ե <

Զ >

3․ Պարզեցնել արտահայտությունը․

Ա √3-1

Բ 5–√5

Գ √3-√2

Դ 4-√10

Թեմա՝ Թվաբանական քառակուսի արմատների հատկությունները։

Դիցուք a≥0, b≥0 և c>0, ապա ճիշտ են հետևյալ հավասարությունները՝

1)√a⋅b=√a⋅√b

2)√a/c=√a/√c

Ցանկացած a իրական թվի համար ճիշտ է՝

3)√a²=|a|

√64⋅81=√64⋅√81−−√=8⋅9=72 √64⋅81=√5184=… =?

Երբեմն հարմար է օգտագործել բերված բանաձևերը հակառակ կարգով, մասնավորապես՝  √a⋅ √b=√a⋅b

Օրինակ՝ Հաշվենք արմատների հետևյալ արտադրյալը՝ 

√2⋅√32=√2⋅32=√64=8 Պատասխան՝ 8

Ակնհայտ է, որ առանձին 2 և 32 թվերից արմատները չէին հանվում, իսկ արտադրյալից՝ հաջողվեց:

Նման կերպ ենք վարվում, երբ չի հաջողվում առանձին հաշվել արմատների հարաբերությունը:

Օրինակ

Հաշվենք արմատների հարաբերությունը:

√75/√3=√75/3=√25=5

Լինում են իրավիճակներ, երբ թիվը քառակուսի բարձրացնելուց հետո, պահանջվում է արդյունքից արմատ հանել:

Այս դեպքերում կարիք չկա առանձին կատարել երկու գործողությունները՝ պատասխանը միանգամից ստացվում է երրորդ հատկության միջոցով:

Օրինակ՝ Այդպես ենք վարվում հետևյալ օրինակներում՝

√5²=5, √92²=92, √(0.67)²=0.67, √(−1.43)²=1.43

Առաջադրանքներ

1․ Ընտրիր ճիշտ հատկությունները:

• √a+√b=√a+b
• √a²=a, a≥0
• √a: √b=√a:b
• √a⋅a =a, a≥0
• √a⋅a=a²

2․ Հաշվել․

Ա 6

Բ 12

Գ 20

Դ 35

Ե 90

Զ 560

3․ Հաշվել․

Ա 20

Բ 18

Գ 30

Ե 48

Զ 105

Է 210

Ը 630

Թ 154

4․ Հաշվել․

Ա 2

Բ 9

Գ x

Դ 3

5․ Հաշվել․

Ա 8

Բ 15

Գ 30

Դ 70

Ե 20

Զ 90

Է 800

Ը 5000

6․ Հաշվել․

Ա 4

Բ 3,1

Գ 1

Դ 5

Ե 1,13

Զ 7,2

Է 0,3

Ը 57,1

7․ Արտադրիչը դուրս բերել արմատանշանի տակից․

Ա √2/3

Բ 3/4

Գ √40/9

Դ √72/5

Ե 5/(√2)

Զ √5/2

Է √x³/3

Ը √7a/4b²

Թ 3m³n²/2a²b

Ժ 5x²y³/mn⁷

Ի √x/10

Լ 5m√2m/√5n

8․ Արտադրիչը դուրս բերել արմատանշանի տակից․

ա)2√3
բ)3√2
գ)2√5
դ)2√6
ե)3√3
զ)2√7
է)4√2
ը)3√5
թ)5√2
ժ)6√2

Թեմա՝ Թվաբանական քառակուսի արմատ։

Տրված a թվից թվաբանական քառակուսի արմատ կոչվում է այն ոչ բացասական թիվը, որի քառակուսին հավասար է տրված a թվին:

Նշանակում ենք այսպես՝ √a: Կարդում ենք՝ a թվից քառակուսի արմատ: 

a -ն թիվն անվանում են արմատատակ թիվ:  

√16=4, քանի որ՝ 4²=16

Ուշադրություն՝ Բացասական թվից քառակուսի արմատ գոյություն չունի:

Օրինակ ՝√-16 արտահայտությունն իմաստ չունի, քանի որ չկա այնպիսի a իրական թիվ, որի քառակուսին հավասար լինի բացասական թվի՝ a²≠−16

Քառակուսի արմատը գտնելու համար պետք է լավ իմանալ թվերի քառակուսիները:

Թվերի հաճախ օգտագործվող քառակուսիներ՝

Հետևաբար, √81=9; √121=11; √361=19 և այլն:

Ուշադրություն՝ √1=1,√0=0

Եթե արմատատակ թիվը տասնորդական կոտորակ է, ապա պետք է ուշադրություն դարձնել ստորակետից հետո եկող թվերի քանակի վրա:

√0,09=0,3; քանի որ 0,3²=0,3⋅0,3=0,09 √0,0016=0,04 √0,009= ?

Այս թիվը բանավոր հաշվել հնարավոր չէ, քանի որ այն անվերջ տասնորդական կոտորակ է:

Եթե արմատատակ թիվը վերջանում է զրոներով, ապա պետք է ուշադրություն դարձնել դրանց քանակի վրա

√400=20 √1210000=1100 √9000=?

Այս թիվը ևս բանավոր հաշվել հնարավոր չէ, քանի որ այն անվերջ տասնորդական կոտորակ է (ստուգիր հաշվիչի օգնությամբ):

Առաջադրանքներ։

1․ Հաշվել քառակուսի արմատը․

√9=3

√16=4

√25=5

√49=7

√81=9

√121=11

√225=15

√289=17

√361=19

√676=26

√484=22

√729=27

√961=31

2․ Հաշվել

Ա 3

Բ 9

Գ 5

Դ 9

Ե 6

Զ 2

Է 4

Ը 1

Թ 1.3

3․ Հաշվել

Ա 18

Բ 3.(33)

Գ 1

Դ 1.2

Ե 0.3

Զ 70

է) 9/3.

ը) 3,6.

թ) 5,2.

4․ Համեմատել

Ա >

Բ <

Գ <

Դ <

Ե >

Զ >

Է <

Ը >

Թ =

5․ Հաշվել

Ա 2

Բ 3

Գ 13

Դ 17

6․ Հաշվել

Ա 30

Բ 18

Գ 2

Դ 6

Ե 2

Զ -3.1

7․ Հաշվել

Ա 7/9

Բ 4/5

Գ 4/3

Դ 3/2

Ե 13/29

8․ Գտնել  արտահայտության արժեքը՝  0.4√0.16+1/2⋅√256

0.4 × 0.4 + 1/2 × 16
0,16 + 8 = 8,16.

Թեմա՝ y=x² ֆունկցիայի հատկությունները և գրաֆիկը։

y=x² ֆունկցիայի գրաֆիկը պարաբոլն է՝

Դիտարկենք գրաֆիկից բխող պարաբոլի որոշ հատկություններ:

1. oy առանցքը հանդիսանում է y=x² պարաբոլի համաչափության առանցք: Համաչափության առանցքը պարաբոլը բաժանում է երկու մասի, որոնք անվանում են պարաբոլի ճյուղեր:
2. Համաչափության oy առանցքը պարաբոլը հատում է որոշակի կետում: Դա այն կետն է, որտեղ միանում են պարաբոլի երկու ճյուղերը: Այն անվանում են պարաբոլի գագաթ:

y=x² պարաբոլը շոշափում է x-երի առանցքը (0;0) կետում:

Եթե նույն կոորդինատային համակարգում կառուցենք  y=x² և y=−x² ֆունկցիաների գրաֆիկները, ապա կնկատենք, որ այդ պարաբոլները համաչափ են իրար x-երի առանցքի նկատմամբ: Դա լավ երևում է ներքևի նկարում:

y=kx² ֆունկցիայի հատկությունները k=1 դեպքում

Ֆունկցիայի հատկությունները նկարագրելիս հիմնվենք նրա գրաֆիկի վրա:

1. y=kx² ֆունկցիան որոշված է x -ի ցանկացած արժեքի համար, այսինքն՝ ֆունկցիայի որոշման տիրույթը ամբողջ (−∞;+∞) թվային առանցքն է:

2. y=0, եթե x=0 և у>0, եթե x≠0: Դա երևում է գրաֆիկից:

3. y=kx² ֆունկցիան աճում է, եթե x≥0 և նվազում է, եթե x≤0

4. Եթե x-ը անսահման տարածվում է դեպի աջ կամ դեպի ձախ (դրական կամ բացասական մնալով), ապա y=kx2 ֆունկցիայի արժեքները դրական մնալով՝ անսահման մեծանում են:

5. y=kx² ֆունկցիայի փոքրագույն արժեքը զրոն է՝ y_min=0, ֆունկցիան այդ արժեքը ընդունում է х=0 դեպքում: Մեծագույն արժեք ֆունկցիան չունի:  

6. y=kx² ֆունկցիան անընդհատ է, քանի որ նրա գրաֆիկը անընդհատ կոր է, որը կարելի է գծել՝ առանց մատիտը թղթից կտրելու:

7. y=kx² (k>0) ֆունկցիան սահմանափակ է ներքևից և սահմանափակ չէ վերևից:

8. y=kx²(k>0) ֆունկցիայի արժեքների բազմությունը [0;+∞) ճառագայթն է:

y=kx² ֆունկցիայի հատկությունները k=-1 դեպքում

1. y=kx² ֆունկցիայի որոշման տիրույթը ամբողջ (−∞;+∞) թվային առանցքն է:

2. y=0, եթե x=0 և у<0, եթե x≠0:

3. y=kx² ֆունկցիան նվազում է, եթե x≥0 և աճում է, եթե x≤0

4. Եթե x-ը անսահման տարածվում է դեպի աջ կամ դեպի ձախ (դրական կամ բացասական մնալով), ապա y=kx² ֆունկցիայի արժեքները բացասական մնալով՝ անսահման մեծանում են մոդուլով:

5. y=kx² ֆունկցիայի մեծագույն արժեքը զրոն է՝ y _min=0, ֆունկցիան այդ արժեքը ընդունում է х=0 դեպքում: Ֆունկցիան փոքրագույն արժեք  չունի:  

6. y=kx² ֆունկցիան անընդհատ է, նրա գրաֆիկը անընդհատ կոր է, որը կարելի է գծել՝ առանց մատիտը թղթից կտրելու:

7. y=kx² (k<0) ֆունկցիան սահմանափակ է վերևից և սահմանափակ չէ ներքևից:

8. y=kx²(k<0) ֆունկցիայի արժեքների բազմությունը (−∞;0] ճառագայթն է:

Առաջադրանքներ։

1․Որոշել y=x² պարաբոլի ճյուղերի ուղղվածությունը:  

• Ճյուղերն ուղղված են դեպի վերև
• Ճյուղերն ուղղված են դեպի ներքև

2․Գտիր y=x² ֆունկցիայի արժեքների բազմությունը: Ընտրել ճիշտ տարբերակը:

• Ֆունկցիան սահմանափակ չէ ներքևից
• Ֆունկցիան սահմանափակ չէ վերևից

3. Տրված է y=−x² ֆունկցիան: Ընտրել ճիշտ պատասխանը:

ա) y_max=−1 բ) y_max=1 գ) y_max=0

4. Տրված է f(x)=−x² ֆունկցիան: Հաշվել  f(−1); f(−5); f(0); f(2); f(4)։

f(-1)=-1

f(-5)=-25

f(0)=0

f(2)=4

f(4)=16

5. Արդյո՞ք  A(3; 8) կետը պատկանում է  y=x²  ֆունկցիայի գրաֆիկին:

ա) չի պատկանում բ) պատկանում է

6. Արդյո՞ք  A(x; y) կետը պատկանում է  y=x² ֆունկցիայի գրաֆիկին, եթե ա) x=1,y=2; բ) x=3, y=9 գ) x=-2; y=4, դ) x=0,4; y=1,6

ա) x=1,y=2; ոչ
բ) x=3, y=9 այո
գ) x=-2; y=4, այո
դ) x=0,4; y=1,6 ոչ

7. Համեմատել թվային արտահայտությունների արժեքները՝ ա) 1,17² < 1,18² բ) 2,31² < 2․33²

8. y=x²  ֆունկցիայի հանար համեմատել y₁ և y₂ , եթե ա) x₁=0,5 x₂=0,6 բ) x₁=9,2 x₂=8,5

ա) x₁=0,5 y₁=0,25
x₂=0,6 y₂=0,36
y₁<y₂
բ) x₁=9,2 y₁=84,64
x₂=8,5 y₂=72,25
y₁>y₂

Թեմա՝ Մեկ անհայտով գծային անհավասարումների համախմբեր։

Տրված են x անհայտով մի քանի անհավասարումներ և հավասարումներ։ Եթե պետք է գտնել բոլոր այն x թվերը, որոնցից յուրաքանչյուրը հանդիսանում է դրանցից մեկի լուծում, ապա ասում են, որ պետք է լուծել մեկ x անհայտով համախումբ։

Համախումբը լուծելու համար պետք է լուծել այդ համախմբի յուրաքանչյուր անհավասարումը կամ հավասարումը և այնուհետև գտնել ստացված լուծումների բազմությունների միավորումը, դա էլ հենց կհանդիսանա տվյալ համախմբի բոլոր լուծումների բազմությունը։

Օրինակ`

Լուծենք 5x – 2 < 3 և 4x + 3 > 0 համախումբը

Լուծում

5x < 5 4x > -3 կստանանք՝

x < 1 x > – 3 / 4

Պատ․՛ ( – ∞ ; 1) ∪ [ – 3/4; + ∞] = ( – ∞ ; +∞)

Այսինքն համախմբի լուծումը՝ բոլոր իրական թվերի համախումբն է՝ R – ը:

Առաջադրանքներ։

1․ 2; 3; -5 թվերից ո՞րն է հետևյալ համախմբի լուծում

Ա 2-ը լուծում է, 3-ը լուծում է, -5-ը լուծում չէ:

Բ 2-ը լուծում չէ, 3-ը -լուծում է, -5-ը լուծում է:

Գ 2-ը լուծում է, 3-լուծում է, -5-ը լուծում է:

2․Լուծել համախումբը․

ա)

3<x

2>x

X(-∞,2)u(3,+∞)

բ)

3<x

5<x

x(-∞,3)u(+5,∞)

գ)

դ)

3․ Գտնել համախմբի լուծումները․

ա)

բ)

գ)

դ)

4․ Լուծել համախումբը․

ա)

բ)

Թեմա՝ Մեկ անհայտով գծային անհավասարումների համակարգեր:

Անհավասարումների համակարգը բաղկացած է մեկ կամ մի քանի անհավասարումներից: Այդ անհավասարումները միավորվում են ձևավոր փակագծով: Պետք է գտնել այդ անհավասարումների բոլոր ընդհանուր լուծումները: 

Փոփոխականի այն արժեքները, որոնց դեպքում համակարգի անհավասարումներից յուրաքանչյուրը վերածվում է ճիշտ անհավասարության, կոչվում են անհավասարությունների համակարգի լուծումներ: 

Գծային անհավասարումների համակարգը լուծելու համար, պետք է լուծել համակարգի յուրաքանչյուր անհավասարումը և այնուհետև գտնել ստացված լուծումների բազմությունների ընդհանուր մասը (հատումը): Դա էլ հենց կլինի համակարգի բոլոր լուծումների բազմությունը:

Լուծել համակարգը՝ նշանակում է գտնել նրա բոլոր լուծումները:

Օրինակ․

Լուծենք հետևյալ համակարգը՝ 

1. Լուծելով առաջին անհավասարումը, ստանում ենք՝

2x>4

x>2

2. Լուծելով երկրորդ անհավասարումը, ստանում ենք՝

3x<13

x<13/3

3. Ստացված միջակայքերը նշենք թվային առանցքի վրա: Յուրաքանչյուրի համար ընտրենք իր նշումը:

4. Անհավասարումների համակարգի լուծումը թվային առանցքի վրա նշված երկու բազմությունների հատումն է:

Մեր դեպքում ստանում ենք այս պատասխանը՝ (2;13/3)

Առաջադրանքներ․

1. Կոորդինատային ուղղի վրա նշեք անհավասարումների համակարգի բոլոր լուծումները (եթե դրանք գոյություն ունեն)․

ա)

x(3;∞)

բ)

x(1;∞)

գ)

x(2;-∞)

դ)

x(-5;-∞)

ե)

x(-7;-5)

զ)

x(-5;0)

2․Փակագծերում նշված թիվը հանդիսանո՞ւմ է արդյոք անհավասարումների համակարգի լուծում՝

ա)

Այո։

բ)

Ոչ։

3․Լուծել անհավասարումների համակարգը

ա) x ∈ (3; -∞);
բ) x ∈ (0; ∞);
գ) x ∈ (-12; 15/4);
դ) x ∈ (−∞, 1/2);
ե) x ∈ (4; ∞);
զ) x ∈ (-∞; 5/3);
է) x ∈ (14/5; ∞);
ը) x ∈ (-∞; -1);

4․Լուծել անհավասարումների համակարգը․

ա)

x ∈ (0.8; ∞);

բ)

x ∈ [2; 4);

գ)

x ∈ (1/5; 1/3);

դ)

x ∈ (0.1; 0.2);

5․Լուծել անհավասարումների համակարգը

ա)

x ∈ [-11; 3);

բ)

x ∈ [4/7; 1);

գ)

x ∈ (-3/2; 0];

դ)

x ∈ (1; 3);

ե)

x ∈ [2; 3);

զ)

x ∈ [2; 3);

Թեմա՝ Ոչ խիստ գծային անհավասարումներ:

kx−b≥0 կամ  kx−b≤0 տեսքի անհավասարումները, որտեղ k -ն և b -ն տրված թվեր են, ընդ որում  k≠0, անվանում են մեկ  x անհայտով առաջին աստիճանի ոչ խիստ անհավասարումներ:

Օրինակ՝ x−3≥2 x≥5 Պատ.՝ x∈[5;+∞)

x անհայտով առաջին աստիճանի գծային անհավասարումները լուծում են ինչպես խիստ գծային անհավասարումները։

Առաջադրանքներ։

1․Լուծել ոչ խիստ գծային անհավասարումները։

Ա Պատ՝. X(-∞,-2]

Բ Պատ՝. X(-∞-1]

Գ Պատ՝. X(-∞,0,8]

Դ Պատ՝.

2․ Լուծել  0.8x ≥−4 գծային անհավասարումը:

3․ x -ի ո՞ր արժեքների դեպքում է 4x−13 երկանդամն ընդունում դրական արժեքներ։

4․ x -ի ո՞ր արժեքների դեպքում է 5x−20 երկանդամն ընդունում ոչ բացասական արժեքներ:

5. k-ի ո՞ր արժեքների դեպքում է −5k+12 երկանդամն ընդունում 2-ից մեծ արժեքներ:

6. Լուծել անհավասարումը՝ ա) 3x−6≤−5x+26 բ) 2x−5<35−6x գ) −4(p+5)≤200 դ) 2(4−3y)+4(9−y)≤60  ե) (x+4)²−x²<5x+13 զ) 5x−4≥−3x−8

7․ -2-ը տրված ոչ խիստ անհավասարումների լուծո՞ւմ է: Պատասխանը հիմնավորել։

ա) 2 + x ≥ 0 բ) 4 + 2x ≤ 0 գ) 7 − x ≤ 0 դ) 9 + 5x ≥ 2 – 3x ե) 4x ≥ −5 + 4x զ) 2(1 + x) ≤ 2x

8․ Լուծել անհավասարումները․

Գիտելիքների ստուգում

1․ Համեմատել թվերը

    ա) -7 < 12         բ)  45 < 56

2․ Մինչև 0,01 ճշտությամբ կլորացնել թվերը և  հաշվել մոտավոր տարբերությունը,  եթե

    ա) a=0,627 b=0,186  բ) a=5,5678 b=-0,2512

Ա 0,63+0,29=0,92 0,63-0,29=0.34 Բ 5,67+(-0,35)=5.32, 5,67-(-0,35)=6.02

3․ Նշել մի որևէ թիվ, որը գտնվում է տրված թվերի միջև  

ա) a=7,6 b=7,7

(7,68)

բ) a=3,8 b=3,(8)  

(3,87)     

4․ Հանել անհավասարության երկու  մասերից միևնույն թիվը.

 ա)  42<56      բ) 12<27

Ա 42-10<56-10

Բ 12-5<27-5

5․ Բազմապատկել անհավասարության երկու    մասը միևնույն բացասական թվով:

    ա) 12<21           բ) 62> 25

Ա 12*(-4)>21*(-4)

Բ 62*(-7)<25*(7)

6․ Գումարել թվային անհավասարությունները։

    ա) 19>10 և 14>7,  բ) -5>-8   և   16>5

Ա.19+14>10+7

Բ. -5+16>-8+5

7․ Կոորդինատային առանցքի վրա  պատկերել հետևյալ միջակայքը

    ա)  [-5;8)       բ) (-9;2]