Category: երկրաչափություն 8

Շրջանագծի մասին տեղեկություն

Շրջանագիծը հարթ երկրաչափության մեջ փակ կոր է, որի բոլոր կետերը հավասար հեռավորության վրա են գտնվում որոշակի կետից, որը կոչվում է կենտրոն։

Շրջանագծի հիմնական տարրերը

• Կենտրոն (O) – Շրջանագծի այն կետը, որից բոլոր կետերը նույն հեռավորության վրա են։
• Շառավիղ (r) – Շրջանագծի կենտրոնից նրա որևէ կետը միացնող հատված։
• Տրամագիծ (d) – Շրջանագծի երկու հակադիր կետեր միացնող և կենտրոնով անցնող հատված ( d=2rd = 2rd=2r )։
• Համայնապատկեր (C) – Շրջանագծի երկարությունը, որը կարելի է գտնել՝ C=2πrC = 2\pi rC=2πr
• Մակերես (S) – Շրջանագծով սահմանված շրջանի մակերեսը՝ S=πr2S = \pi r^2S=πr2
• Խորանարդային աղեղ – Շրջանագծի մի մասը, որը սահմանվում է երկու կետով։
• Հատված (հատվածային մակերես) – Շրջանագծի մի մաս, որը սահմանվում է աղեղով և դրա երկու ծայրակետերը միացնող քորդայով։

Եռանկյան մասին տեղեկություն

Եռանկյունը հարթ երկրաչափության պարզագույն բազմակողմանիքներից (պոլիգոններից) մեկն է, որն ունի երեք կողմ, երեք գագաթ և երեք անկյուն։

---

Եռանկյան հիմնական տարրերը

• Գագաթներ – Եռանկյան երեք կետերը, որոնք միացվում են կողմերով։
• Կողմեր – Գագաթները միացնող հատվածները։
• Անկյուններ – Կողմերի միջև գոյացած անկյունները։

---

Եռանկյան տեսակները

1️⃣ Կողմերի երկարությամբ

• Հավասարակողմ եռանկյուն – Բոլոր երեք կողմերը հավասար են։
• Հավասարասրուն եռանկյուն – Երկու կողմերը հավասար են, իսկ երրորդը՝ տարբեր։
• Տարբերակողմ եռանկյուն – Բոլոր կողմերը տարբեր են։

2️⃣ Անկյունների մեծությամբ

• Սուրանկյուն եռանկյուն – Բոլոր անկյունները փոքր են 90°-ից։
• Ուղղանկյուն եռանկյուն – Մեկ անկյունը 90° է։
• Թվանկյուն եռանկյուն – Մեկ անկյունը մեծ է 90°-ից։

---

Եռանկյան հիմնական բանաձևերը

✅ Պարագիծ (P) P=a+b+cP = a + b + cP=a+b+c

(որտեղ a,b,ca, b, ca,b,c – եռանկյան կողմերն են)

✅ Մակերես (S)

• Ըստ Հերոնի բանաձևի (եթե կողմերը հայտնի են)՝ S=s(s−a)(s−b)(s−c)S = \sqrt{s(s-a)(s-b)(s-c)}S=s(s−a)(s−b)(s−c)​ (որտեղ s=a+b+c2s = \frac{a+b+c}{2}s=2a+b+c​ կիսապարագիծն է)
• Ուղղանկյուն եռանկյան դեպքում S=12abS = \frac{1}{2}abS=21​ab (որտեղ aaa և bbb ուղղանկյուն եռանկյան կապող կողմերն են)

✅ Ներագծված և արտագծված շրջանագծերի շառավիղներ

• Ներագծված շրջանագծի շառավիղ՝ r=Ssr = \frac{S}{s}r=sS​
• Արտագծված շրջանագծի շառավիղ՝ R=abc4SR = \frac{abc}{4S}R=4Sabc​

Քառանկյան մասին տեղեկություն

Քառանկյունի (քառակողմի) մասին ընդհանուր տեղեկություններ

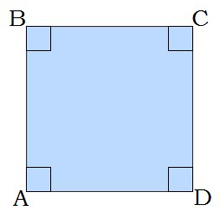
Քառանկյունը երկրաչափական պատկեր է, որը կազմված է չորս գագաթից և չորս կողմից։ Այն կարող է լինել տարբեր ձևերի և հատկությունների՝ կախված կողմերի ու անկյունների հարաբերություններից։

---

Քառանկյան հիմնական տարրերը

• Գագաթներ – Չորս կետեր, որոնք կազմում են քառանկյունի սահմանները։
• Կողմեր – Գագաթները միացնող հատվածները։
• Անկյուններ – Կողմերի միջև առաջացած անկյունները։
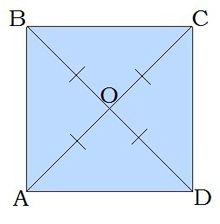
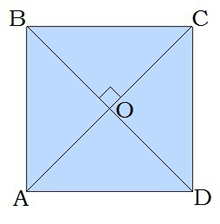
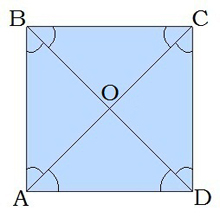
• Ալիքներ (Անկյունագծեր) – Քառանկյան հակադիր գագաթները միացնող հատվածներ։

1․ Ո՞ր պատկերն է կոչվում շրջանագիծ:

2. Ի՞նչ է շրջանագծի շառավիղ, տրամագիծը, լարն ու աղեղը:

3․ GEOGEBRA ծրագրով գծել շրջանագիծ և տանել նրա շառավիղը, տրամագիծը և լարը:

4․ Գրել լարի միջնակետով անցնող շառավղի հատկությունները:

5․ Թվարկել   շրջանագծի բոլոր  տրամագծերը,   շառավիղները և  լարերը:

6․ Թվարկել ստացված աղեղները:

7․ Քանի՞ անգամ է շրջանագծի տրամագիծը մեծ նրա շառավղից։

8․ Ողիղը հատում է շրջանագիծը A և B կետերում։ Ի՞նչ կետերով պիտի անցնի այդ ուղիղը, որպեսզի AB հատվածն ունենա հնարավոր ամենամեծ երկարությունը։

9․ Հաշվել CA -ն, եթե CD=8 սմ և ∠AOD=120°

10․ Տրված է՝ MN=7սմ,  ∠ONM=60°։Գտնել KN-ը։

11․ AB հատվածը O կենտրոնով շրջանագծի տրամագիծն է, իսկ AC-ն և BC -ն այդ շրջանագծի հավասար լարեր են։ Գտնել AOC անկյունը։

Թեմա՝ Բուրգ

Հին աշխարհի յոթ հրաշալիքներից են Եգիպտական բուրգերը:

Բուրգերի հաճախ ենք հանդիպում նաև հայկական ճարտարապետական կոթողներում:

Մասնավորապես, եկեղեցիներից շատերի գմբեթներն ունեն բուրգի տեսք:

Բուրգն  այն  բազմանիստն  է, որի  նիստերից  մեկը  բազմանկյուն  է, իսկ  մյուս  բոլոր նիստերն  ընդհանուր  գագաթով  եռանկյուններ  են:

Բազմանկյունը  կոչվում  է  բուրգի  հիմք, եռանկյունները՝  կողմնային  նիստեր ,իսկ եռանկյունների  ընդհանուր  գագաթը՝  բուրգի  գագաթ։ Բուրգի գագաթը հիմքի բազմանկյան գագաթներին միացնող հատվածները կոչվում են կողմնային կողեր, իսկ գագաթի հանդիպակաց կողմերը՝ հիմքի կողեր։

Բուրգի գագաթից հիմքի հարթությանն իջեցված ուղղահայացը կոչվում է բուրգի բարձրություն:

 Բուրգը, կախված  հիմքի  բազմանկյան  կողմերի  թվից, կոչվում  է  եռանկյուն  բուրգ, քառանկյուն  բուրգ,  հնգանկյուն  բուրգ  և  այլն։

n-անկյուն բուրգն ունի 2n կող (n-ը հիմքի կողերն են, n-ը՝ կողմնային կողերը), n+1 գագաթ  և  n+1 նիստ։

Բուրգը  նշանակելու համար սկզբում  գրվում է գագաթի տառը, այնուհետև՝ հիմքի բազմանկյան գագաթների տառերը։

Հարցեր և առաջադրանքներ։

1.Ո՞ր մարմինն է կոչվում  բուրգ։

Բուրգն  այն  բազմանիստն  է, որի  նիստերից  մեկը  բազմանկյուն  է, իսկ  մյուս  բոլոր նիստերն  ընդհանուր  գագաթով  եռանկյուններ  են:

2.GEOGEBRA ծրագրով գծիր  բուրգ։

3.Ո՞ր նիստերն են կոչվում հիմքեր, կողմնային նիստեր:

n-անկյուն բուրգն ունի 2n կող (n-ը հիմքի կողերն են, n-ը՝ կողմնային կողերը), n+1 գագաթ  և  n+1 նիստ։

4․Գտեք վեցանկյան բուրգի կողերի, գագաթների, նիստերի քանակը,

Կողեր – 2 * 6 = 12
Գագաթներ – 6 + 1 = 7
Նիստեր – 6 + 1 = 7

GEOGEBRA     ծրագրով գծեք վեցանկյուն բուրգ:

5․Կարո՞ղ է բուրգի կողերի թիվը լինել՝

ա) 13
Ոչ, քանի որ 16-ը չի բաժանվում երկուսի։

բ) 16
Այո, քանի որ 16-ը բաժանվում է երկուսի։

գ) 19։    
Ոչ, քանի որ 19-ը չի բաժանվում երկուսի։

Պատասխանը հիմնավորել։

6․Կարո՞ղ է լինել այնպիսի բուրգ, որն ունի ՝

ա) 9 նիստ,      
Այո, քանի որ 9-ից հանել մեկ հնարավոր է։

բ)  9 կող։    
Ոչ, քանի որ 9-ը երկուսի չի բաժանվում։

Պատասխանը հիմնավորել։

7․ Ինչպե՞ս է կոչվում այն բուրգը, եթե այն ունի

ա) 13 նիստ – Տասներկուանկյուն բուրգ
բ) 10 գագաթ –  Իննանկյուն բուրգ 
գ) 12 կող – Վեցանկյուն բուրգ։

8․Քառանկյուն բուրգի հիմքը 64 սմ պարագծով քառակուսի է,իսկ կողմնային նիստերը հավասարակողմ եռանկյուններ են։ Գտեք բուրգի կողմնային կողերը։
64սմ / 4 = 16սմ
16սմ * 3 = 48սմ
48սմ * 4 = 192սմ։

Թեմա՝ Տարածական պատկերներ։ Զուգահեռանիստ

Երկրաչափության այն բաժինը, որը ուսումնասիրում է պատկերների հատկությունները տարածության մեջ, կոչվում է տարածաչափություն:

Այն պատկերը, որի ոչ բոլոր կետերն են ընկած միևնույն հարթության մեջ, կոչվում է  տարածական պատկեր:

Տարածության սահմանափակված մասը կոչվում է երկրաչափական կամ տարածաչափական մարմին, իսկ մարմինը սահմանափակող կետերի բազմությունը՝ մարմնի մակերևույթ:

Գունդը երկրաչափական մարմին է, գնդոլորտը նրա մակերևույթն է:

Պարուրաձև գիծը տարածական պատկեր է: Սակայն այն մարմին չէ:

պարուրաձև գիծ

Բուրգը երկրաչափական մարմին է, որը սահմանափակված է բազմանկյուններով:

Բազմանիստի մակերևույթը կազմող բազմանկյունները կոչվում են բազմանիստի նիստեր:

Նիստերի կողմերը կոչվում են բազմանիստի կողեր:

Կողերի ծայրակետերը կոչվում են բազմանիստի գագաթներ:

Զուգահեռանիստի սահմանումն ու հատկությունները

Զուգահեռանիստ կոչվում է այն բազմանիսը, որի բոլոր 6 նիստերը զուգահեռագծեր են:

Զուգահեռանիստն ունի 6 նիստ, 8 գագաթ և 12 կող:

Զուգահեռանիստի ընդհանուր կող ունեցող նիստերը կոչվում են կից, իսկ ընդհանուր կողեր չունեցող նիստերը՝ հանդիպակաց:

Զուգահեռանիստի հիմքեր անվանում են նիա որևէ երկու հանդիպակաց նիստերը, իսկ մնացած նիստերը՝ կողմնային նիստեր: 

Հիմքերին չպատկանող կողերը կոչվում են զուգահեռանիստի կողմնային կողեր: 

Նույն նիստում չգտնվող երկու գագաթները միացնող հատվածը կոչվում է զուգահեռագծի  անկյունագիծ: 

Զուգահեռանիստի հատկությունները:

— Զուգահեռանիստի հանդիպակաց նիստերը զուգահեռ են և հավասար:

— Զուգահեռանիստի բոլոր չորս անկյունագծերը հատվում են միևնույն կետում և այդ կետում կիսվում են: 

Հարցեր և առաջադրանքներ։

1․ Ո՞ր պատկերն է կոչվում տարածական մարմին կամ տարածական պատկեր։ Դրանք այն պատկերներն են, որոնց եթե դնենք սեղանի վրա նրանք ամբողջովին չեն դիպչի սեղանին:

2․ GEOGEBRA ծրագրով գծել տարածական մարմին։

3․ Ի՞նչ է բազմանիստը։

Բազմանիստ, բազմանկուններով կազմված փակ մակերևույթ, նրան երբեմն անվանում են այդ մակերևույթով սահմանափակված մարմին։

4․ Ո՞ր պատկերն է կոչվում զուգահեռանիստ, GEOGEBRA ծրագրով գծել զուգահեռանիստ։

5․ Զուգահեռանիստը քանի՞ նիստ, քանի՞ կող, քանի՞ գագաթ ունի։

Զուգահեռանիստը ունի 6 նիստ, 16 կող, 8 գագաթ:

6․ Բազմանիստների և նրանց տարրերի մասին բերված պնդումներից (սահմանումներից) ո՞րն է ճիշտ: Ընտրել ճիշտ տարբերակ(ներ)ը:

Եթե տարածական մարմնի մակերևույթը կազմված է ուղղանկյուններից, ապա այն կոչվում է բազմանիստ:

Բազմանիստի մակերևույթը կազմող բազմանկյունները կոչվում են բազմանիստի նիստեր:

Նիստերի կողմերը կոչվում են բազմանիստի կողեր:

Եթե տարածաչափական մարմնի մակերևույթը բաղկացած է բազմանկյուններից, ապա մարմինը բազմանիստ է:

7․ Զուգահեռանիստի մասին թվարկված պնդումներից ո՞րն է ճիշտ: Ընտրել ճիշտ պնդումը:

Զուգահեռանիստի հիմքը զուգահեռագիծ է:

Զուգահեռանիստ կոչվում է այն պրիզման, որի կողմնային նիստերը չորս ուղղանկյուններ են:

Զուգահեռանիստի նիստերը վեց ուղղանկյուններ են:

8․ Բերվածնկարներից ո՞րն է զուգահեռանիստը: Նշել  ճիշտ պատասխանը: 3-րդ պատկերն է:

9․ Գրել զուգահեռանիստի հատկությունները։

Զուգահեռանիստի հատկությունները:

— Զուգահեռանիստի հանդիպակաց նիստերը զուգահեռ են և հավասար:

— Զուգահեռանիստի բոլոր չորս անկյունագծերը հատվում են միևնույն կետում և այդ կետում կիսվում են: 

10․ ABCDA₁B₁C₁D₁ զուգահեռանիստի մեջ գտնել B₁C₁ -ը և DC-ն, եթե BC=7 սմ, A₁B₁=5 սմ:

B₁C₁=7սմ
DC=5սմ

1. O կետը AL հատվածը բաժանում է երկու հավասար մասերի: Գտնել  հատվածի միջնակետի նկատմամբ համաչափ կետեր:

A և L

B և K

C և J

D և I

E և H

2. Տրված է AL հատվածը: Գտնել D կետի նկատմամբ համաչափ կետերը:

D=I

3. Ո՞ր կետն է C կետին համաչափ՝ (0;−4) կետի նկատմամբ:

C=H

4. Գտնել Оx առանցքի նկատմամբ B կետին համաչափ կետը:

B=F

Թեմա՝ Քառակուսի։

Քառակուսի է կոչվում այն ուղղանկյունը, որի բոլոր կողմերը հավասար են:

Քառակուսու հատկությունները

Քառակուսին զուգահեռագիծ է, ուղղանկյուն և շեղանկյուն: Հետևաբար, այն ունի զուգահեռագծի, ուղղանկյան և շեղանկյան բոլոր հատկությունները:

1. Քառակուսու բոլոր կողմերը հավասար են՝ AB=BC=CD=AD:

2. Քառակուսու բոլոր անկյունները 90° են:

3. Քառակուսու անկյունագծերը հավասար են և հատման կետով կիսվում են՝ BD=AC; BO=OD=AO=OC:

4. Քառակուսու անկյունագծերը փոխուղղահայաց են՝ BD⊥AC:

5. Քառակուսու անկյունագծերը նաև անկյունների կիսորդներ են՝ ∢ABD=∢DBC=∢BCA=…=45°:

6. Անկյունագիծը քառակուսին բաժանում է չորս հավասար հավասարասրուն ուղղանկյուն եռանկյունների:  

Հարցեր և առաջադրանքներ։

1․ Ո՞ր պատկերն է կոչվում քառակուսի։ GEOGEBRA ծրագրով գծել ABCD քառակուսի։

2․ Գրել քառակուսու հատկությունները։

Քառակուսու բոլոր կողմերը իրար հավասար են, քառակուսու բոլոր անկյուններն 90° են:

3․ Տրված է՝ OC=23 սմ: Գտնել DB-ն։

լուծում՝ 23*2=46

Պատ.՝ DB=46

4․ Քառակուսու կողմը 15 սմ է։ Գտնել քառակուսու պարագիծը։

Լուծում՝ 15*4=60 սմ

Պատ՝. 60 սմ

5․Քառակուսու պարագիծը 72 սմ է: Հաշվել քառակուսու կողմը:

Լուծում՝ 72/4=18 սմ

Պատ.՝ 18 սմ

6․ Քառակուսու անկյունագծերի հատման կետից մինչև բոլոր կողմերը եղած հեռավորությունների գումարը 24 սմ է: Գտեք քառակուսու պարագիծը:

լուծում՝ 24:4=6սմ, 6*2=12, 12*4=48

1. Գտեք ABC եռանկյան  C անկյունը, եթե
ա) ∠A=68⁰, ∠B=53⁰ 68+53=121, 180-121=59, C=59
ա) ∠A=25⁰, ∠B=110⁰։ 25+110=135, 180-135=45, C=45

2.Գտեք ABC եռանկյան անկյունները, եթե <A:<B:<C=2:3:4

2+3+4=9

180:9=20

20․2=40

20․3=60

20․4=80

40,60,80
3. Հավասարասրուն եռանկյան արտաքին անկյուններից մեկը 110⁰ է։ Գտեք եռանկյան անկյունները։ Դիտարկել բոլոր հնարավոր դեպքերը։

4․ Նկարում ∠4=∠5։ Զուգահեռ են արդյո՞ք a և b ուղիղները։

5․ Գտնել ∠1-ը, եթե m || n

6. Գտնել հավասարասրուն ուղղանկյուն եռանկյան բոլոր անկյունները։
7. Ուղղանկյուն եռանկյան սուր անկյուններից մեկը 60⁰ է, իսկ ներքնաձիգը 26 սմ։ Գտնել փոքր էջի երկարությունը։