Թեմա՝ Քառակուսային հավասարման գաղափարը։ Թերի քառակուսային հավասարումներ։
ax2+bx+c=0 տեսքի հավասարումը, որտեղ a -ն, b -ն և c -ն տրված թվեր են, և a≠0, անվանում են քառակուսային (քառակուսի) հավասարում:
Օրինակ
2x2+3x−8=0, −3x2+2x+1=0, x2+5x=0, 2x2−4=0, 25x2=0 հավասարումները քառակուսային հավասարումների օրինակներ են:
a թիվն անվանում են ավագ անդամի՝ x2 -ու գործակից, b թիվը՝ x -ի գործակից, c -ն՝ ազատ անդամ:
Քանի որ a≠0, ապա ցանկացած քառակուսային հավասարում ունի ax2 ավագ անդամը: Այդ պատճառով քառակուսային հավասարումն անվանում են նաև երկրորդ աստիճանի հավասարում:
Քառակուսային հավասարման ուսումնասիրման հարցերում կարևոր դեր է խաղում հետևյալ թիվը՝ D=b2−4ac
D=b2−4ac թիվն անվանում են ax2+bx+c=0 քառակուսային հավասարման տարբերիչ կամ՝ դիսկրիմինանտ:
Օրինակ
1) 2x2−3x−5=0 հավասարման մեջ a=2 -ը x2 -ու գործակիցն է, b=−3 -ը՝ x -ի գործակիցը, իսկ c=−5 -ը՝ ազատ անդամը: Հաշվենք տարբերիչը` D=(−3)2−4⋅2⋅(−5)=9+40=49
2) x2−7=0 հավասարման մեջ b=0, այդ պատճառով էլ չկա x պարունակող անդամը: x2 -ու գործակիցը a=1 -ն է, իսկ ազատ անդամը՝ c=−7: Տարբերիչը հավասար է՝ D=−4⋅(−7)=28
Հիշենք, որ
x անհայտով հավասարման արմատ կամ լուծում անվանում են այն թիվը, որը հավասարման մեջ x -ի փոխարեն տեղադրելով ստացվում է ճիշտ թվային հավասարություն:
Լուծել հավասարումը՝ նշանակում է գտնել նրա բոլոր արմատները կամ ցույց տալ, որ արմատներ չկան:
Ուշադրություն
Եթե ax2+bx+c=0 տեսքի հավասարման մեջ a=0, այսինքն, չկա x2 պարունակող անդամը, ապա հավասարումը քառակուսային չէ:
Վերջին երեք օրինակներում a≠0 (այսինքն, դրանք քառակուսային հավասարումներ են), սակայն՝
x2+2x=0 հավասարման մեջ c=0
2x2−6=0 հավասարման մեջ b=0
12x2=0 հավասարման մեջ երկուսն էլ զրո են՝ b=0, c=0
Այս օրինակներում բերվածները կոչվում են թերի հավասարումներ:
Քառակուսային հավասարումը կոչվում է թերի, եթե b և c թվերից գոնե մեկը հավասար է զրոյի:
Օրինակ
Լուծենք հետևյալ թերի հավասարումները՝
1) x2+3x=0
x2+3x=0 x(x+3)=0 x=0 x=−3
Պատասխան՝ x1=0, x2=−3
2) 2x2−8=0
2x2−8=0 x2−4=0 (x−2)(x+2)=0 x1=2 x2=−2
Պատասխան՝ x1=2,x2=−2
3) 7x2=0
7x2=0, x2=0, x=0
Պատասխան՝ x=0
Հարցեր և առաջադրանքներ։
1․ Ո՞ր հավասարումն է կոչվում քառակուսային։
ax2+bx+c=0 տեսքի հավասարումը, որտեղ a -ն, b -ն և c -ն տրված թվեր են, և a≠0, անվանում են քառակուսային (քառակուսի) հավասարում:
2․ Ինչպե՞ս են հաշվում քառակուսային հավասարման տարբերիչը։
D=b2−4ac
1) 2x2−3x−5=0 հավասարման մեջ a=2 -ը x2 -ու գործակիցն է, b=−3 -ը՝ x -ի գործակիցը, իսկ c=−5 -ը՝ ազատ անդամը: Հաշվենք տարբերիչը` D=(−3)2−4⋅2⋅(−5)=9+40=49
2) x2−7=0 հավասարման մեջ b=0, այդ պատճառով էլ չկա x պարունակող անդամը: x2 -ու գործակիցը a=1 -ն է, իսկ ազատ անդամը՝ c=−7: Տարբերիչը հավասար է՝ D=−4⋅(−7)=28
3․ Ո՞ր հավասարումն է կոչվում թերի քառակուսային։
Քառակուսային հավասարումը կոչվում է թերի, եթե b և c թվերից գոնե մեկը հավասար է զրոյի:
4․ Կազմել ax2+bx+c=0 քառակուսային հավասարում, եթե նրա գործակիցները հավասար են․

Ա 3x2+4x+5=0
Բ 3x2-2x+6=0
Գ x2-x+2=0
Դ -x2+3x-2=0
5․ Հաշվել քառակուսային հավասարման տարբերիչը․

Ա 49
Բ 21
Գ 0
Դ -3
6․ Ստուգել՝ 0 թիվը հավասարման արմա՞տ է․

Ա այո
Բ ոչ
Գ ոչ
Դ ոչ
Ե այո
Զ ոչ
Լուծել հավասարումները․

Ա x(-1;1)
Բ 0
Գ x(0;1)
Դ x(0;-3)
Ե x(-2;3)
Զ x(-5;7)
Է x(0;0.5)
Ը x(0;-2)
Թ x(-5;8)
Ժ x(-1;4)
7․ Լուծել հավասարումները․
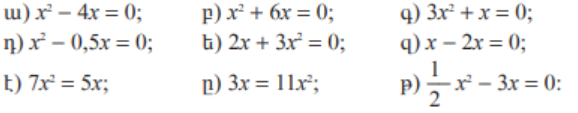
Ա x(0;4)
Բ x(-6;0)
Գ x(-1/3;0)
Դ x(0;0.5)
Ե x(-2/3;0)
Զ 0
Է x(0;5/7)
Ը x(0;3/11)
Թ x(0;6)
8․ Լուծել հավասարումները․

Ա x(-√3;√3)
Բ x(-√5;√5)
Գ x(-√3;√3)
Դ x(-√50;√50)
Ե x(-√3/2;-√3/2)
Զ լուծում չունի
Է x(-48;48)
Ը x(-5.6;5.6)
Թ x(-√200;√200)