Թեմա` Պարզագույն իռացիոնալ հավասարումների լուժումը:
Եթե հավասարման անհայտը գտնվում է քառակուսի արմատի նշանի տակ, ապա այդպիսի հավասարումը անվանում են իռացիոնալ:
Կյանքի շատ իրավիճակներ նկարագրվում են իռացիոնալ հավասարումներով: Ուստի, սովորենք լուծել գոնե պարզագույն իռացիոնալ հավասարումները:
Դիտարկենք
Եթե հավասարման անհայտը գտնվում է քառակուսի արմատի նշանի տակ, ապա այդպիսի հավասարումը անվանում են իռացիոնալ:
Կյանքի շատ իրավիճակներ նկարագրվում են իռացիոնալ հավասարումներով: Ուստի, սովորենք լուծել գոնե պարզագույն իռացիոնալ հավասարումները:
Դիտարկենք √2x+1=3 իռացիոնալ հավասարումը:
Ըստ քառակուսի արմատի սահմանման, այն նշանակում է, որ 2x+1=32: Փաստորեն, քառակուսի բարձրացնելով, տրված իռացիոնալ հավասարումը բերեցինք 2x+1=9 գծային հավասարմանը:
Ուշադրություն
Քառակուսի բարձրացնելը իռացիոնալ հավասարումների լուծման հիմնական եղանակն է:
Դա բնական է, եթե պետք է ազատվել քառակուսի արմատի նշանից:
2x+1=9 հավասարումից ստանում ենք՝ x=4: Սա միաժամանակ 2х+1=9 գծային և √2x+1=3 իռացիոնալ հավասարումների արմատն է:
Քառակուսի բարձրացնելու եղանակը տեխնիկապես բարդ չէ իրականացնել, սակայն երբեմն այն բերում է անցանկալի իրավիճակների:
Օրինակ
Դիտարկենք √2x−5=√4x−7 իռացիոնալ հավասարումը:
Երկու մասերը բարձրացնելով քառակուսի, ստանում ենք՝ (√2x−5)2=(√4x−7)2 2x−5=4x−7
Լուծելով ստացված 2x−4x=−7+5 հավասարումը, ստանում ենք x=1
Սակայն x=1, որը 2x−5=4x−7 գծային հավասարման արմատն է, չի բավարարում տրված իռացիոնալ հավասարմանը: Ինչո՞ւ: Իռացիոնալ հավասարման մեջ փոխարեն տեղադրենք 1: Կստանանք՝ √−3=√−3
Հավասարումը բնականաբար չի բավարարվում, քանի որ հավասարության ձախ և աջ մասերը իմաստ չունեն։
Ստացել ենք ավելորդ արմատ: Այսպիսի իրավիճակներում ասում ենք, որ x=1 -ը թույլատրելի արժեք չէ, կամ չի պատկանում թույլատրելի արժեքների բազմությանը: Դուրս եկավ, որ այս դեպքում, իռացիոնալ հավասարումը արմատ չունի, մինչդեռ քառակուսի բարձրացնելուց ստացված գծային հավասարումը արմատ ուներ:
Պետք է այսպիսի ավելորդ արմատները ժամանակին հայտնաբերել և չընդգրկել լուծումների մեջ՝ դեն նետել: Դա արվում է ստուգման միջոցով:
Իռացիոնալ հավասարումների համար, ստուգումը լուծման անհրաժեշտ փուլ է, որը օգնում է հայտնաբերել և դեն նետել ավելորդ արմատնելը:
Ուշադրություն
Այսպիսով, իռացիոնալ հավասարումը լուծելու համար պետք է՝
1) այն բարձրացնել քառակուսի,
2) լուծել ստացված հավասարումը,
3) կատարել ստուգում՝ դեն նետելով ավելորդ արմատները,
4) գրել վերջնական պատասխանը:
Կիրառելով այս եզրակացությունը, դիտարկենք հետևյալ օրինակը:
Օրինակ
Լուծենք √5x−16=2 հավասարումը:
1) Երկու մասերը բարձրացնենք քառակուսի՝ (√5x−16)2=22
2) Լուծենք ստացված հավասարումը՝
5x−16=4 5x=20 x=4
3) Կատարենք ստուգում: √5x−16=2 հավասարման մեջ տեղադրենք x=4: Ստանում ենք՝ √4=2 ճիշտ հավասարությունը:
4) Պատասխան՝ √5x−16=2 հավասարման լուծումը x=4 -ն է:
Հարցեր և առաջադրանքներ։
1․Ո՞ր հավասարումներն են կոչվում իռացիոնալ։
Եթե հավասարման անհայտը գտնվում է քառակուսի արմատի նշանի տակ, ապա այդպիսի հավասարումը անվանում են իռացիոնալ:
2․ Ինչպե՞ս են լուծում պարզագույն իռացիոնալ հավասարումները։
1) այն բարձրացնել քառակուսի,
2) լուծել ստացված հավասարումը,
3) կատարել ստուգում՝ դեն նետելով ավելորդ արմատները,
4) գրել վերջնական պատասխանը:
3․ Լուծել հավասարումները։

Ա x=9
Բ x=0
Գ լուծում չունի
Դ 0,5
Ե 0,5
զ) -1
է) 44/3
ը) 48/5
թ) 7
4․ Լուծել հավասարումները։
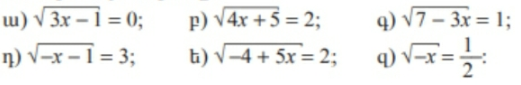
ա) x=1/3a^2+1/3
բ) լուծում չունի
գ) x=2
դ) լուծում չունի
ե) x=8/5
զ) լուծում չունի
5․ Լուծել հավասարումները․

249.x=4
250.x=9
251.x=25
252.∅
253.x=0
254.x=81
255.x=64
256.∅
257.x=25
258.x=0
259.∅
260.x=25
261.x=6
262.x=20
263.x=6
264.x=6
265.∅
266.x=9
267.x=4,5
268.x=10
269.x=1
270.∅
271.x=3,3
272.x=1,3
273.x=6
274.∅
275.∅
276.x=7
277.∅
278.x=10
279.∅
280.x=0,75