Պարապմունք 44

Թեմա՝ Թվաբանական քառակուսի արմատների հատկությունները։

Դիցուք a≥0, b≥0 և c>0, ապա ճիշտ են հետևյալ հավասարությունները՝

1)√a⋅b=√a⋅√b

2)√a/c=√a/√c

Ցանկացած a իրական թվի համար ճիշտ է՝

3)√a²=|a|

√64⋅81=√64⋅√81−−√=8⋅9=72 √64⋅81=√5184=… =?

Երբեմն հարմար է օգտագործել բերված բանաձևերը հակառակ կարգով, մասնավորապես՝  √a⋅ √b=√a⋅b

Օրինակ՝ Հաշվենք արմատների հետևյալ արտադրյալը՝ 

√2⋅√32=√2⋅32=√64=8 Պատասխան՝ 8

Ակնհայտ է, որ առանձին 2 և 32 թվերից արմատները չէին հանվում, իսկ արտադրյալից՝ հաջողվեց:

Նման կերպ ենք վարվում, երբ չի հաջողվում առանձին հաշվել արմատների հարաբերությունը:

Օրինակ

Հաշվենք արմատների հարաբերությունը:

√75/√3=√75/3=√25=5

Լինում են իրավիճակներ, երբ թիվը քառակուսի բարձրացնելուց հետո, պահանջվում է արդյունքից արմատ հանել:

Այս դեպքերում կարիք չկա առանձին կատարել երկու գործողությունները՝ պատասխանը միանգամից ստացվում է երրորդ հատկության միջոցով:

Օրինակ՝ Այդպես ենք վարվում հետևյալ օրինակներում՝

√5²=5, √92²=92, √(0.67)²=0.67, √(−1.43)²=1.43

Առաջադրանքներ

1․ Ընտրիր ճիշտ հատկությունները:

• √a+√b=√a+b
• √a²=a, a≥0
• √a: √b=√a:b
• √a⋅a =a, a≥0
• √a⋅a=a²

2․ Հաշվել․

Ա 6

Բ 12

Գ 20

Դ 35

Ե 90

Զ 560

3․ Հաշվել․

Ա 20

Բ 18

Գ 30

Ե 48

Զ 105

Է 210

Ը 630

Թ 154

4․ Հաշվել․

Ա 2

Բ 9

Գ x

Դ 3

5․ Հաշվել․

Ա 8

Բ 15

Գ 30

Դ 70

Ե 20

Զ 90

Է 800

Ը 5000

6․ Հաշվել․

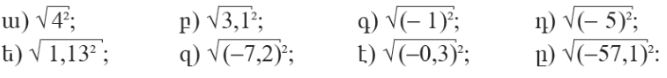
Ա 4

Բ 3,1

Գ 1

Դ 5

Ե 1,13

Զ 7,2

Է 0,3

Ը 57,1

7․ Արտադրիչը դուրս բերել արմատանշանի տակից․

Ա √2/3

Բ 3/4

Գ √40/9

Դ √72/5

Ե 5/(√2)

Զ √5/2

Է √x³/3

Ը √7a/4b²

Թ 3m³n²/2a²b

Ժ 5x²y³/mn⁷

Ի √x/10

Լ 5m√2m/√5n

8․ Արտադրիչը դուրս բերել արմատանշանի տակից․

ա)2√3
բ)3√2
գ)2√5
դ)2√6
ե)3√3
զ)2√7
է)4√2
ը)3√5
թ)5√2
ժ)6√2